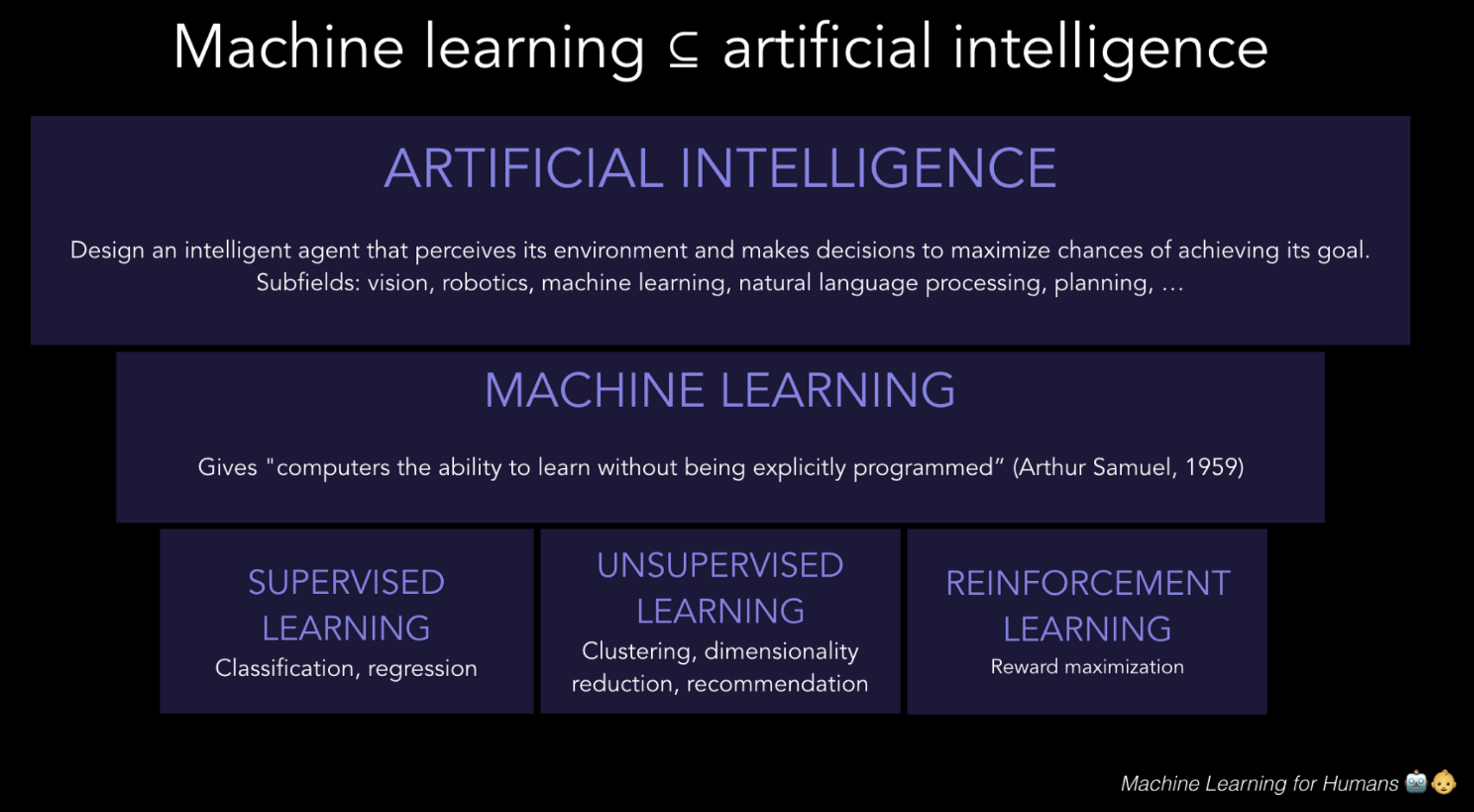
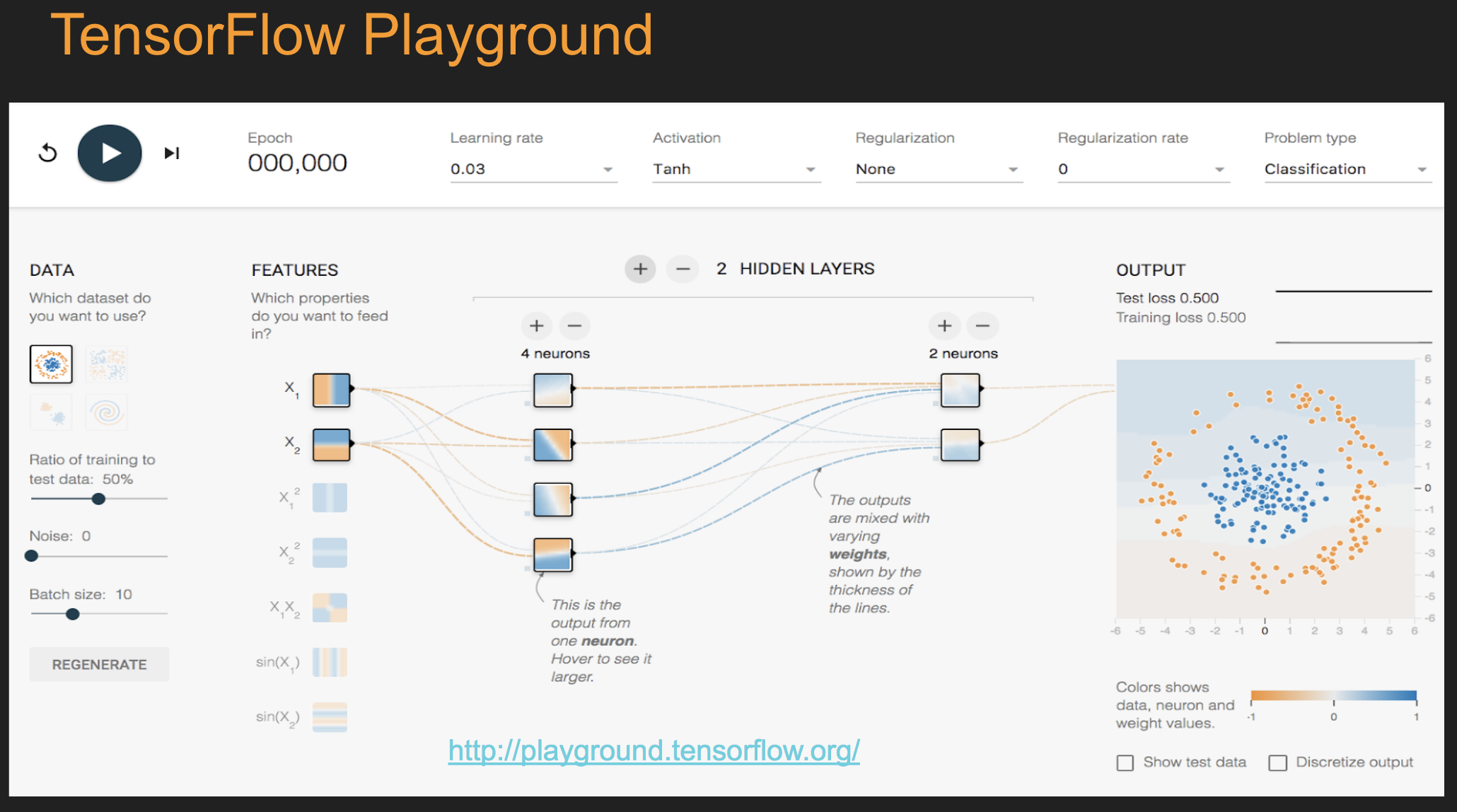
Deep Learning¶
Sanjiv R. Das¶
Professor of Finance and Data Science¶
Santa Clara University¶
REFERENCE BOOK: http://srdas.github.io/DLBook
In [1]:
%pylab inline
import pandas as pd
from IPython.external import mathjax
Populating the interactive namespace from numpy and matplotlib
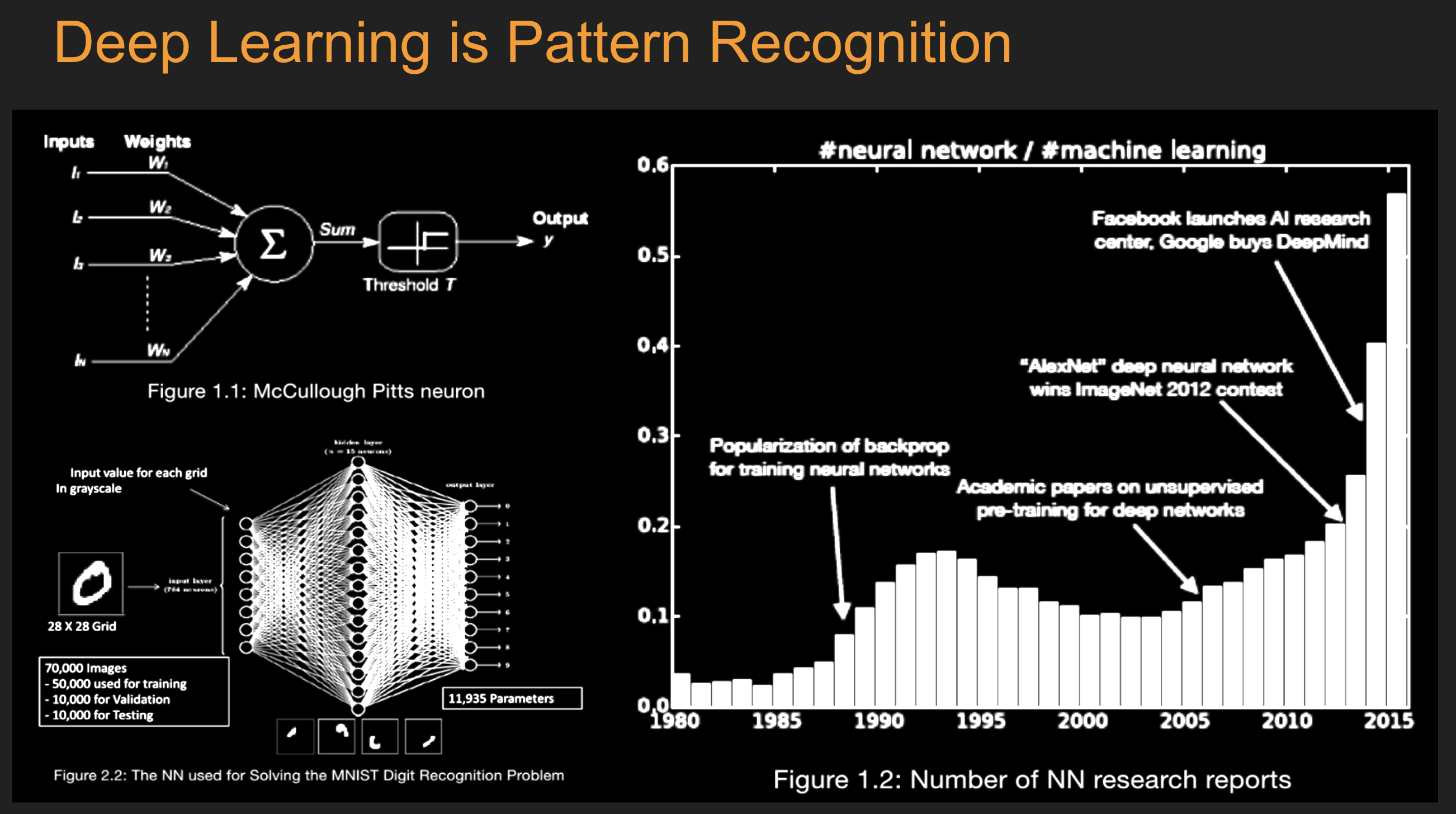
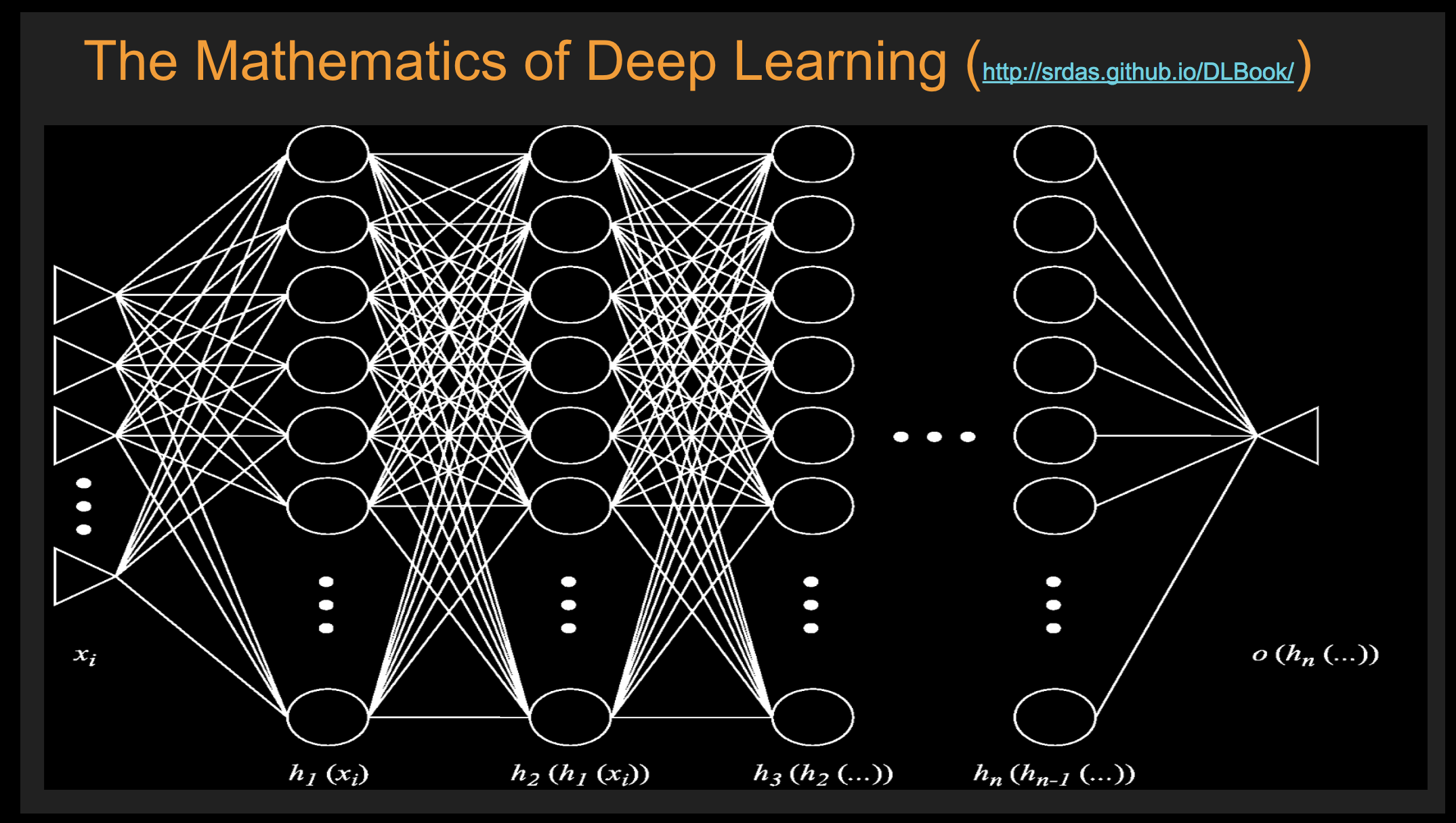
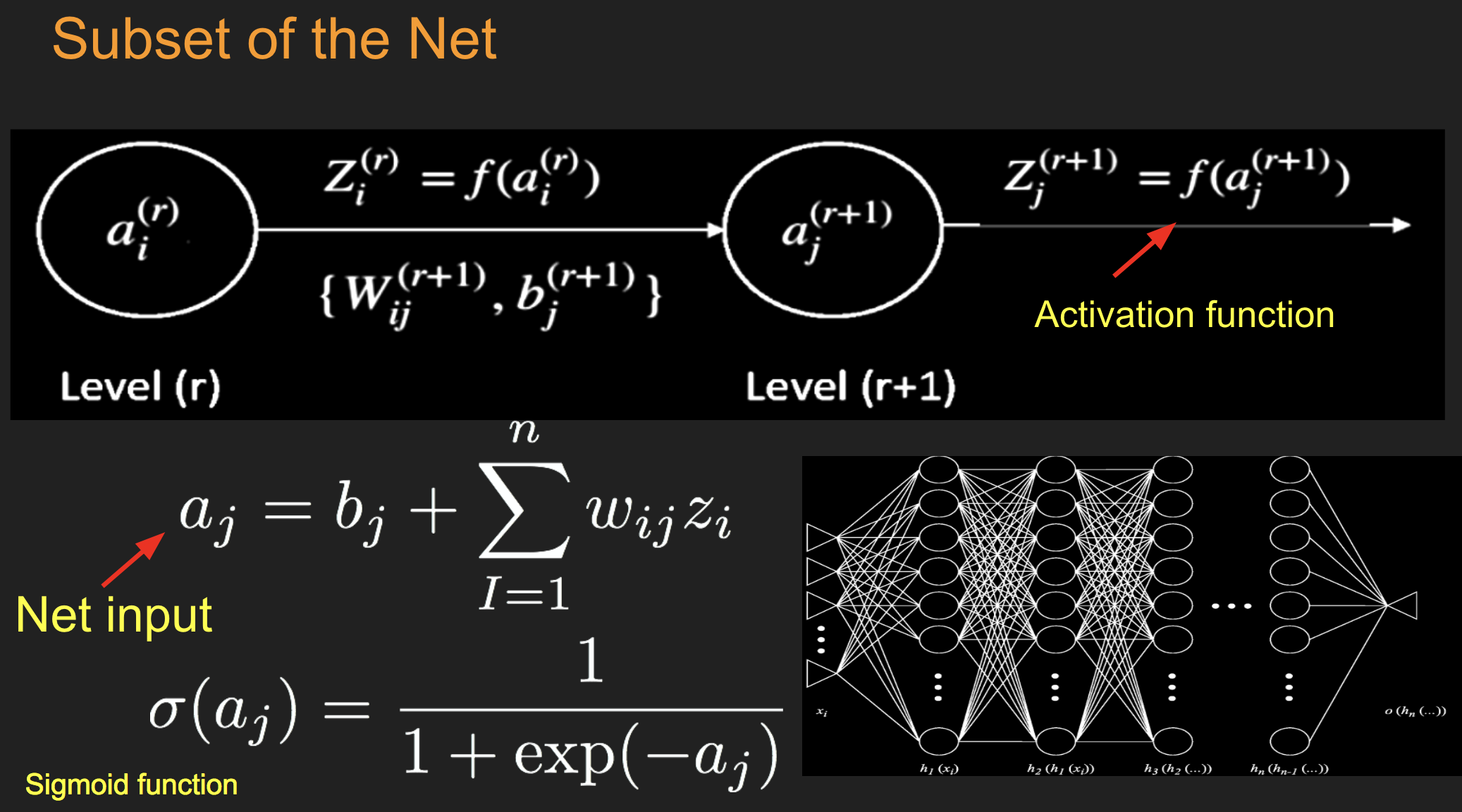
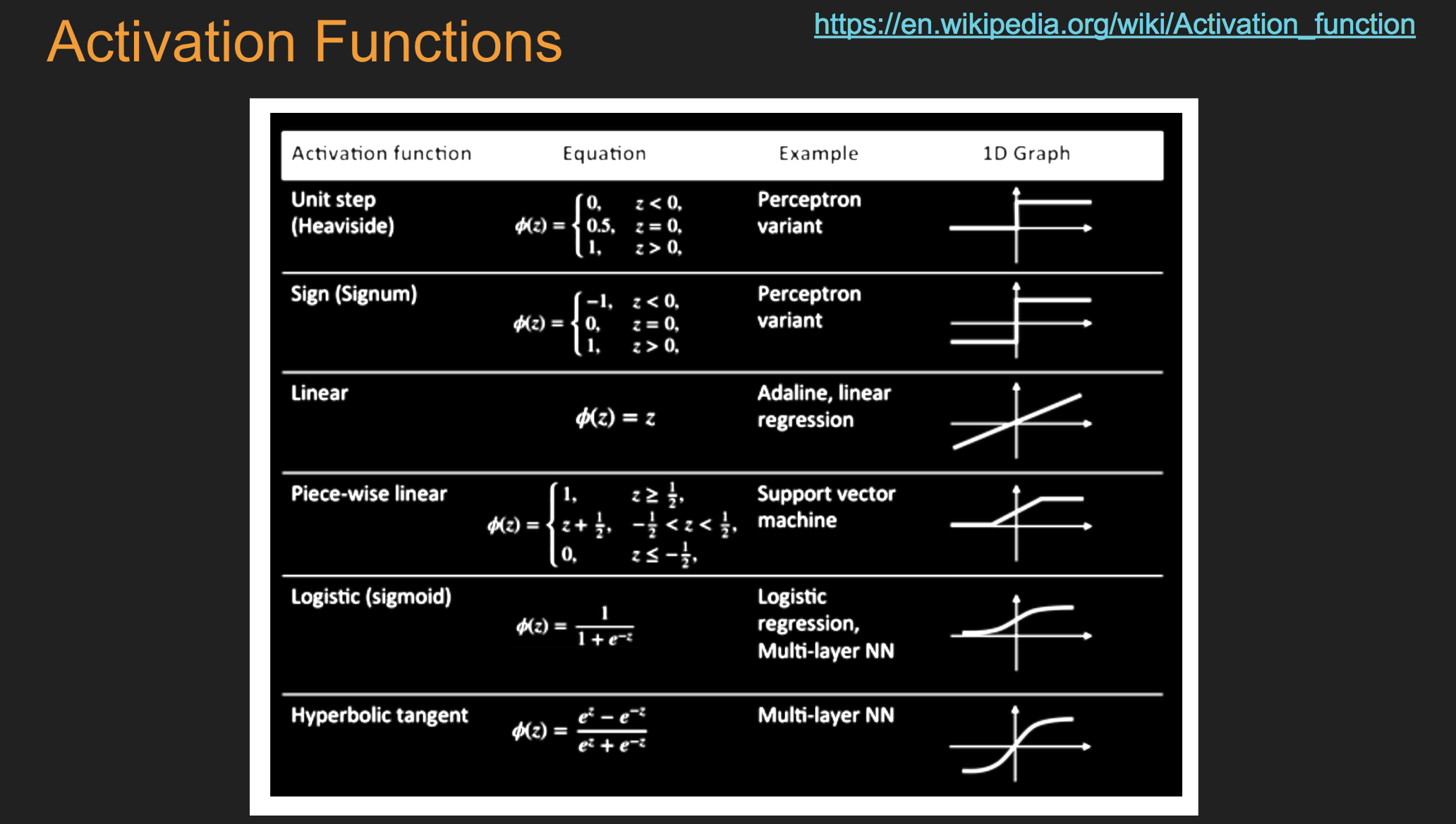
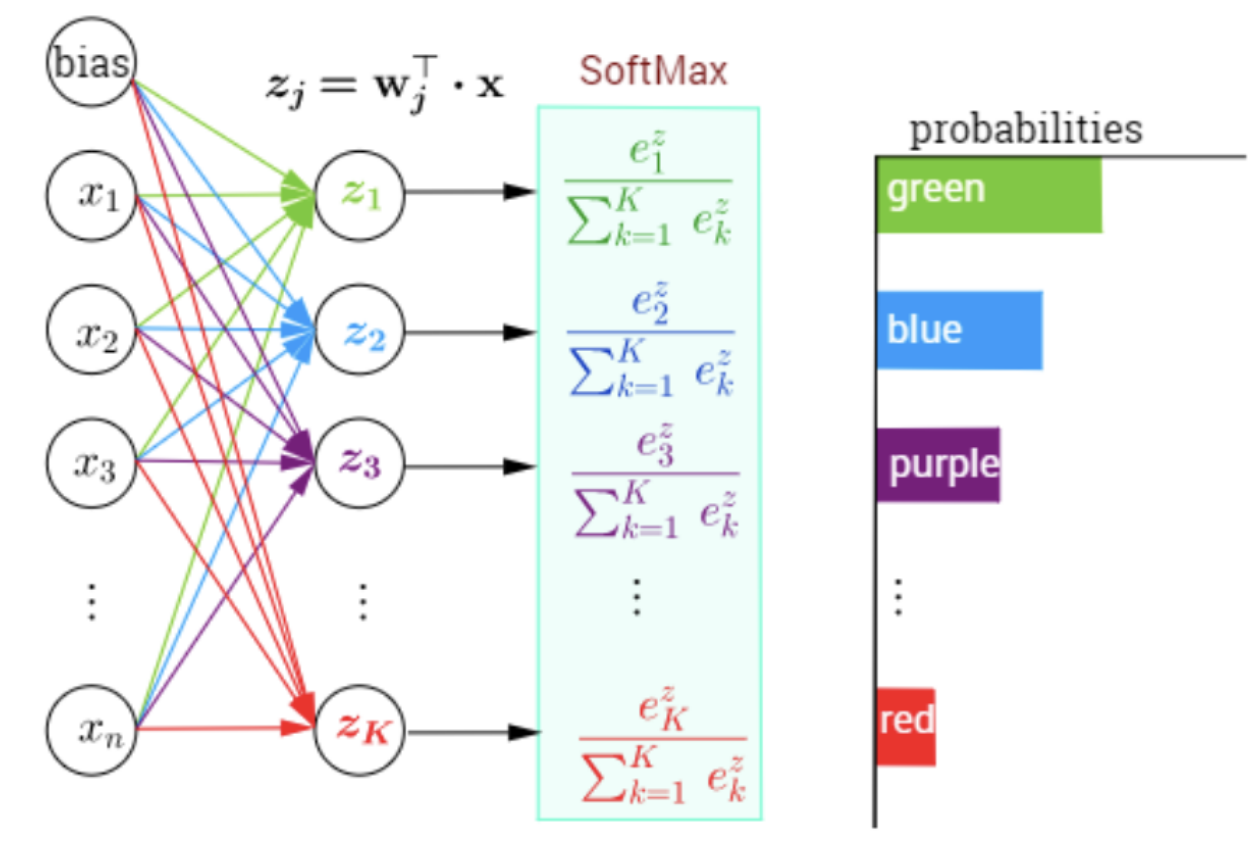


Batch Stochastic Gradient¶
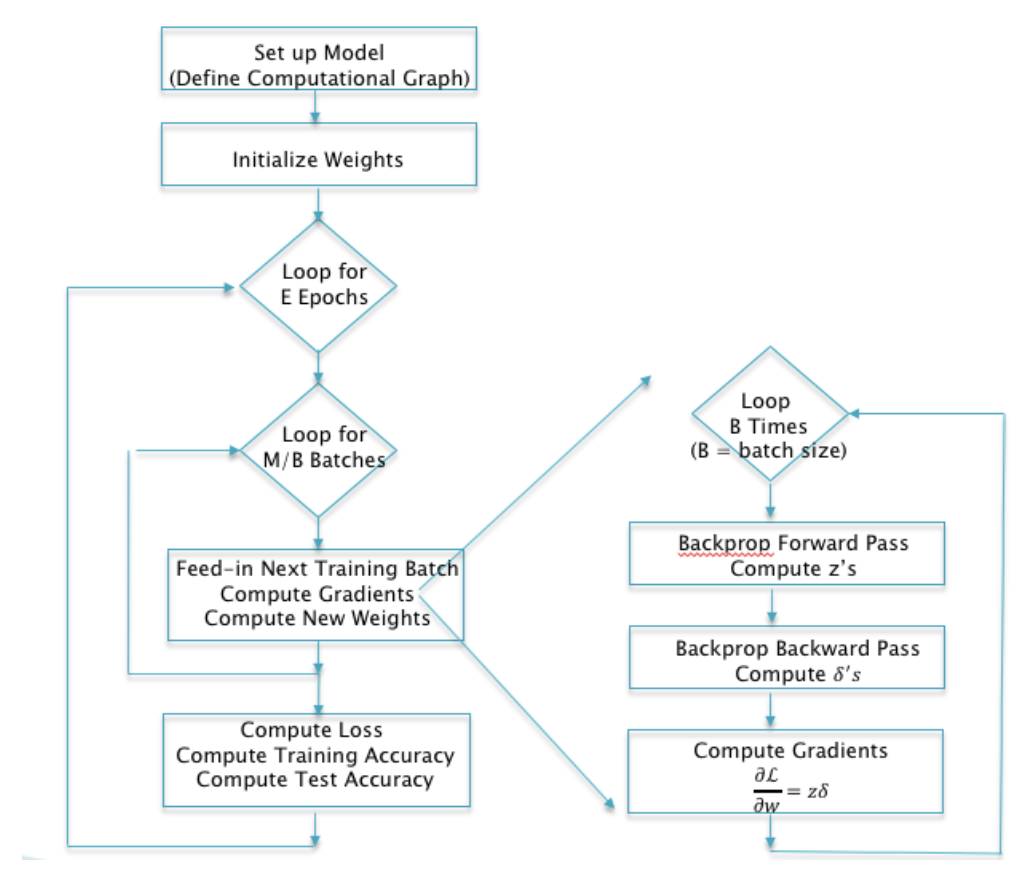
Gradient Descent Example¶
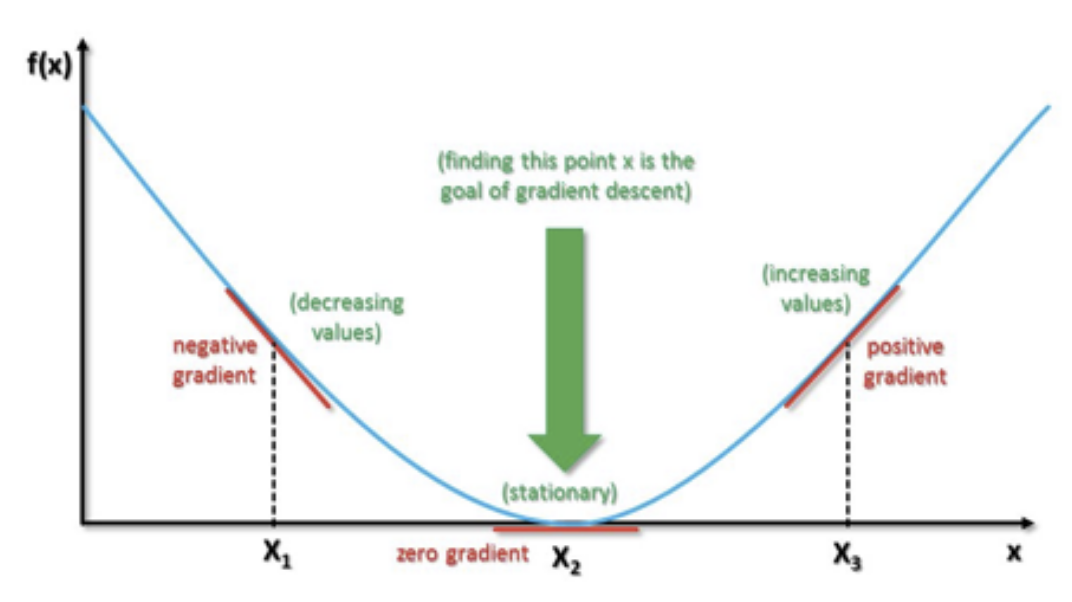
In [2]:
def f(x):
return 3*x**2 -5*x + 10
x = linspace(-4,4,100)
plot(x,f(x))
grid()
In [3]:
dx = 0.001
eta = 0.05 #learning rate
x = -3
for j in range(20):
df_dx = (f(x+dx)-f(x))/dx
x = x - eta*df_dx
print(x,f(x))
-1.8501500000001698 29.519915067502733 -1.0452550000002532 18.503949045077853 -0.4818285000003115 13.105618610239208 -0.08742995000019249 10.460081738472072 0.18864903499989083 9.163520200219716 0.3819043244999847 8.528031116715445 0.5171830271499616 8.216519714966186 0.6118781190049631 8.06379390252634 0.6781646833034642 7.988898596522943 0.7245652783124417 7.95215813604575 0.7570456948186948 7.934126078037087 0.7797819863730542 7.925269906950447 0.7956973904611502 7.920916059254301 0.8068381733227685 7.918772647178622 0.8146367213259147 7.917715356568335 0.8200957049281836 7.917192371084045 0.8239169934497053 7.916932669037079 0.8265918954147882 7.9168030076222955 0.8284643267903373 7.916737788340814 0.8297750287532573 7.916704651261121



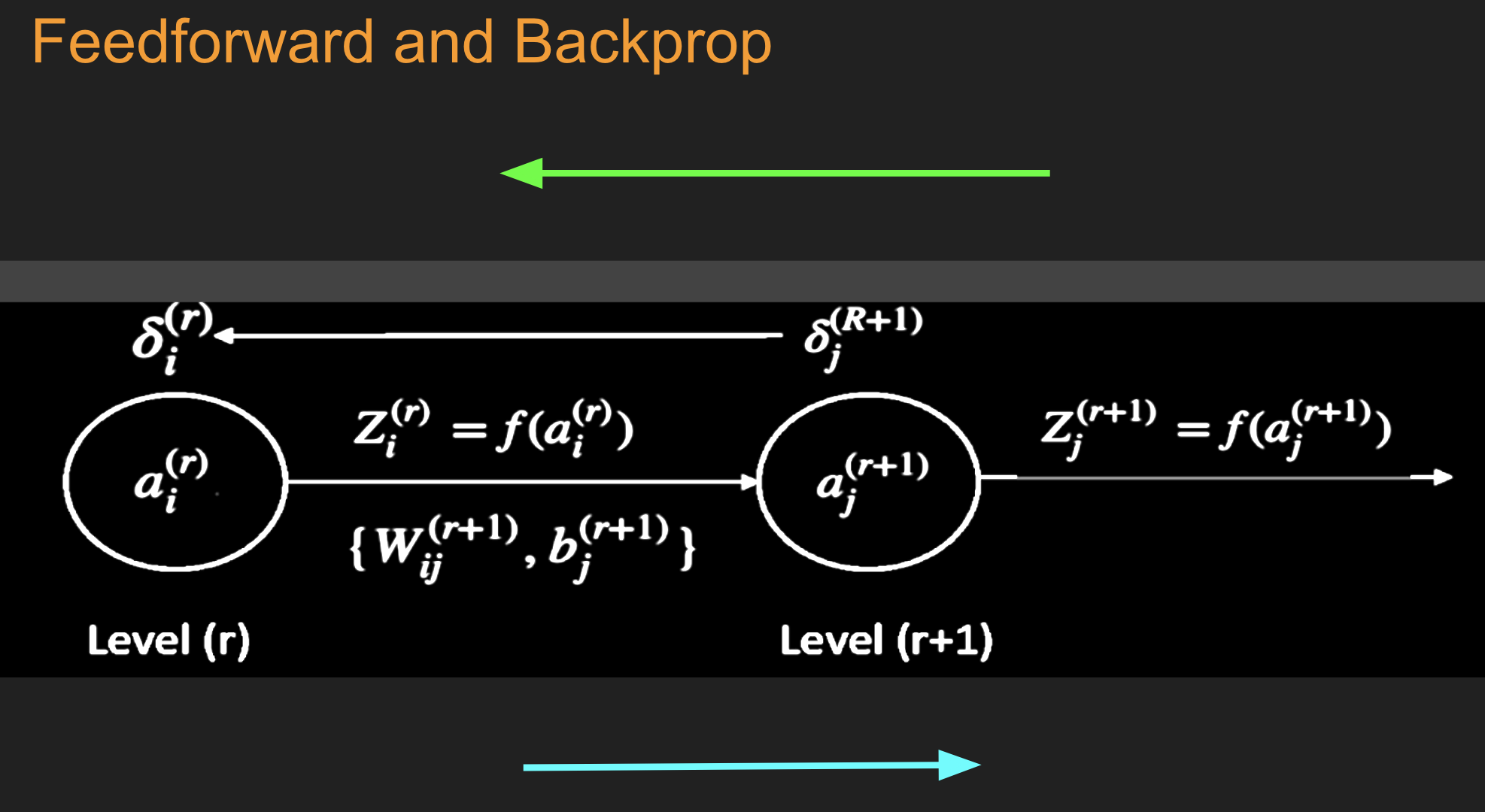
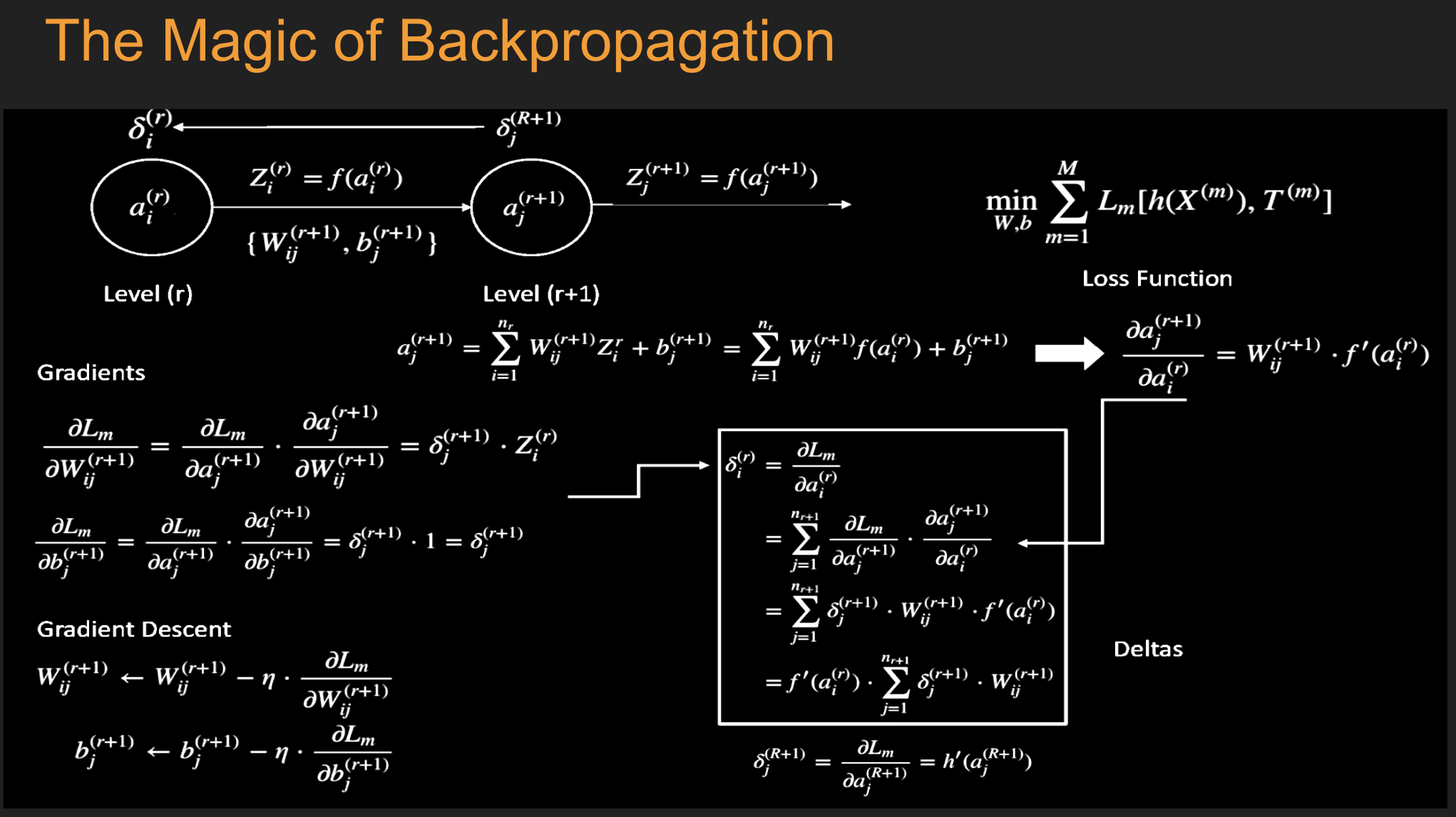
Under and Over-fitting¶
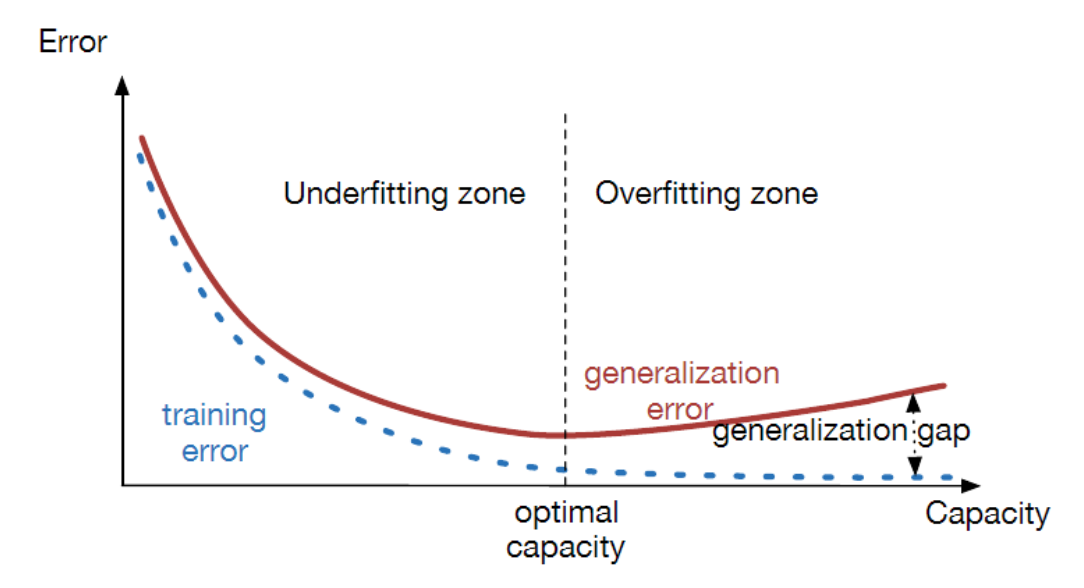
Dropout regularization¶
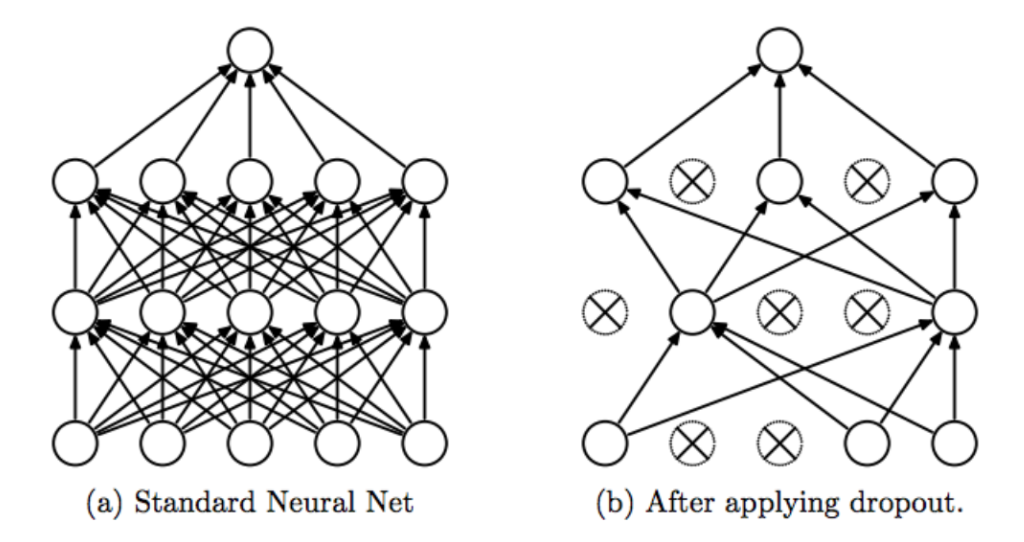
Pattern Recognition: Cancer¶
In [7]:
## Read in the data set
data = pd.read_csv("data/BreastCancer.csv")
data.head()
Out[7]:
| Id | Cl.thickness | Cell.size | Cell.shape | Marg.adhesion | Epith.c.size | Bare.nuclei | Bl.cromatin | Normal.nucleoli | Mitoses | Class | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1000025 | 5 | 1 | 1 | 1 | 2 | 1 | 3 | 1 | 1 | benign |
| 1 | 1002945 | 5 | 4 | 4 | 5 | 7 | 10 | 3 | 2 | 1 | benign |
| 2 | 1015425 | 3 | 1 | 1 | 1 | 2 | 2 | 3 | 1 | 1 | benign |
| 3 | 1016277 | 6 | 8 | 8 | 1 | 3 | 4 | 3 | 7 | 1 | benign |
| 4 | 1017023 | 4 | 1 | 1 | 3 | 2 | 1 | 3 | 1 | 1 | benign |
In [9]:
## Convert the class variable into binary numeric
ynum = zeros((len(x),1))
for j in arange(len(y)):
if y[j]=="malignant":
ynum[j]=1
ynum[:10]
Out[9]:
array([[0.],
[0.],
[0.],
[0.],
[0.],
[1.],
[0.],
[0.],
[0.],
[0.]])
In [10]:
## Make label data have 1-shape, 1=malignant
from keras import utils
y.labels = utils.to_categorical(ynum, num_classes=2)
#x = x.as_matrix()
print(y.labels[:10])
print(shape(x))
print(shape(y.labels))
print(shape(ynum))
/Users/sdas/anaconda3/lib/python3.6/site-packages/h5py/__init__.py:34: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`. from ._conv import register_converters as _register_converters Using TensorFlow backend.
[[1. 0.] [1. 0.] [1. 0.] [1. 0.] [1. 0.] [0. 1.] [1. 0.] [1. 0.] [1. 0.] [1. 0.]] (683, 9) (683, 2) (683, 1)
In [11]:
## Define the neural net and compile it
from keras.models import Sequential
from keras.layers import Dense, Activation
model = Sequential()
model.add(Dense(32, activation='relu', input_dim=9))
model.add(Dense(32, activation='relu'))
model.add(Dense(32, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
In [12]:
## Fit/train the model (x,y need to be matrices)
model.fit(x, ynum, epochs=25, batch_size=32,verbose=2)
Epoch 1/25 - 0s - loss: 0.6031 - acc: 0.7233 Epoch 2/25 - 0s - loss: 0.4522 - acc: 0.8931 Epoch 3/25 - 0s - loss: 0.3719 - acc: 0.9063 Epoch 4/25 - 0s - loss: 0.3167 - acc: 0.9122 Epoch 5/25 - 0s - loss: 0.2762 - acc: 0.9297 Epoch 6/25 - 0s - loss: 0.2450 - acc: 0.9444 Epoch 7/25 - 0s - loss: 0.2197 - acc: 0.9502 Epoch 8/25 - 0s - loss: 0.1979 - acc: 0.9488 Epoch 9/25 - 0s - loss: 0.1793 - acc: 0.9546 Epoch 10/25 - 0s - loss: 0.1652 - acc: 0.9590 Epoch 11/25 - 0s - loss: 0.1515 - acc: 0.9649 Epoch 12/25 - 0s - loss: 0.1385 - acc: 0.9663 Epoch 13/25 - 0s - loss: 0.1294 - acc: 0.9693 Epoch 14/25 - 0s - loss: 0.1284 - acc: 0.9663 Epoch 15/25 - 0s - loss: 0.1180 - acc: 0.9693 Epoch 16/25 - 0s - loss: 0.1133 - acc: 0.9722 Epoch 17/25 - 0s - loss: 0.1117 - acc: 0.9722 Epoch 18/25 - 0s - loss: 0.1032 - acc: 0.9736 Epoch 19/25 - 0s - loss: 0.0994 - acc: 0.9693 Epoch 20/25 - 0s - loss: 0.0954 - acc: 0.9663 Epoch 21/25 - 0s - loss: 0.0891 - acc: 0.9736 Epoch 22/25 - 0s - loss: 0.0882 - acc: 0.9736 Epoch 23/25 - 0s - loss: 0.0816 - acc: 0.9780 Epoch 24/25 - 0s - loss: 0.0825 - acc: 0.9766 Epoch 25/25 - 0s - loss: 0.0784 - acc: 0.9795
Out[12]:
<keras.callbacks.History at 0x1124c1d68>
In [13]:
## Accuracy
yhat = model.predict_classes(x, batch_size=32)
acc = sum(yhat==ynum)
print("Accuracy = ",acc/len(ynum))
## Confusion matrix
from sklearn.metrics import confusion_matrix
confusion_matrix(yhat,ynum)
Accuracy = 0.9795021961932651
Out[13]:
array([[431, 1],
[ 13, 238]])
Another Canonical Example: Digit Recognition (MNIST)¶
- Extensible to many finance prediction problems.
- Information set: 784 (28 x 28) pixels for category prediction.
- Would you run a multinomial regression on these 784 columns.

In [14]:
## Read in the data set
train = pd.read_csv("data/train.csv", header=None)
test = pd.read_csv("data/test.csv", header=None)
print(shape(train))
print(shape(test))
(60000, 785) (10000, 785)
In [15]:
## Reformat the data
X_train = train.as_matrix()[:,0:784]
Y_train = train.as_matrix()[:,784:785]
print(shape(X_train))
print(shape(Y_train))
X_test = test.as_matrix()[:,0:784]
Y_test = test.as_matrix()[:,784:785]
print(shape(X_test))
print(shape(Y_test))
y.labels = utils.to_categorical(Y_train, num_classes=10)
print(shape(y.labels))
print(y.labels[1:5,:])
print(Y_train[1:5])
(60000, 784) (60000, 1) (10000, 784) (10000, 1) (60000, 10) [[0. 0. 0. 1. 0. 0. 0. 0. 0. 0.] [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]] [[3] [0] [0] [2]]
In [16]:
hist(Y_train); grid()
In [17]:
## Define the neural net and compile it
from keras.models import Sequential
from keras.layers import Dense, Activation, Dropout
from keras.optimizers import SGD
data_dim = shape(X_train)[1]
model = Sequential([
Dense(100, input_shape=(784,)),
Activation('sigmoid'),
Dense(100),
Activation('sigmoid'),
Dense(100),
Activation('sigmoid'),
Dense(100),
Activation('sigmoid'),
Dense(10),
Activation('softmax'),
])
#model = Sequential()
#model.add(Dense(100, activation='sigmoid', input_dim=data_dim))
#model.add(Dropout(0.25))
#model.add(Dense(100, activation='sigmoid'))
#model.add(Dropout(0.25))
#model.add(Dense(100, activation='sigmoid'))
#model.add(Dropout(0.25))
#model.add(Dense(100, activation='sigmoid'))
#model.add(Dropout(0.25))
#model.add(Dense(10, activation='softmax'))
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
In [18]:
## Fit/train the model (x,y need to be matrices)
model.fit(X_train, y.labels, epochs=10, batch_size=32,verbose=2)
Epoch 1/10 - 5s - loss: 0.7642 - acc: 0.7631 Epoch 2/10 - 5s - loss: 0.3575 - acc: 0.8957 Epoch 3/10 - 5s - loss: 0.2835 - acc: 0.9160 Epoch 4/10 - 5s - loss: 0.2495 - acc: 0.9262 Epoch 5/10 - 5s - loss: 0.2310 - acc: 0.9311 Epoch 6/10 - 5s - loss: 0.2096 - acc: 0.9371 Epoch 7/10 - 5s - loss: 0.2010 - acc: 0.9400 Epoch 8/10 - 5s - loss: 0.1940 - acc: 0.9409 Epoch 9/10 - 5s - loss: 0.1869 - acc: 0.9437 Epoch 10/10 - 5s - loss: 0.1850 - acc: 0.9443
Out[18]:
<keras.callbacks.History at 0x114b70908>
In [19]:
## In Sample
yhat = model.predict_classes(X_train, batch_size=32)
## Confusion matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(yhat,Y_train)
print(" ")
print(cm)
##
acc = sum(diag(cm))/len(Y_train)
print("Accuracy = ",acc)
[[5769 0 49 19 11 44 26 13 29 27] [ 0 6507 16 15 8 6 9 15 73 8] [ 7 49 5528 128 8 11 2 45 53 5] [ 7 22 54 5600 1 94 1 20 89 40] [ 17 19 99 7 5671 19 26 99 49 303] [ 24 19 20 157 4 5114 57 18 84 31] [ 46 10 81 11 37 64 5784 0 36 5] [ 2 16 46 51 2 5 0 5916 10 48] [ 47 77 56 91 7 28 13 7 5324 43] [ 4 23 9 52 93 36 0 132 104 5439]] Accuracy = 0.9442
In [20]:
## Out of Sample
yhat = model.predict_classes(X_test, batch_size=32)
## Confusion matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(yhat,Y_test)
print(" ")
print(cm)
##
acc = sum(diag(cm))/len(Y_test)
print("Accuracy = ",acc)
[[ 961 0 10 3 2 8 11 2 5 6] [ 0 1108 1 2 0 1 2 6 4 5] [ 0 4 959 16 4 3 0 15 7 0] [ 1 2 10 932 0 19 0 7 17 9] [ 2 1 14 1 954 2 3 8 10 55] [ 2 1 2 27 0 835 10 3 16 3] [ 7 3 13 0 6 11 928 0 10 1] [ 1 3 8 9 0 3 0 953 4 7] [ 6 13 11 12 2 4 4 1 891 11] [ 0 0 4 8 14 6 0 33 10 912]] Accuracy = 0.9433
Learning the Black-Scholes Equation¶
See : Hutchinson, Lo, Poggio (1994)
In [23]:
from scipy.stats import norm
def BSM(S,K,T,sig,rf,dv,cp): #cp = {+1.0 (calls), -1.0 (puts)}
d1 = (math.log(S/K)+(rf-dv+0.5*sig**2)*T)/(sig*math.sqrt(T))
d2 = d1 - sig*math.sqrt(T)
return cp*S*math.exp(-dv*T)*norm.cdf(d1*cp) - cp*K*math.exp(-rf*T)*norm.cdf(d2*cp)
df = pd.read_csv('data/training.csv')
Normalizing spot and call prices¶
$C$ is homogeneous degree one, so $$ aC(S,K) = C(aS,aK) $$ This means we can normalize spot and call prices and remove a variable by dividing by $K$. $$ \frac{C(S,K)}{K} = C(S/K,1) $$
In [24]:
df['Stock Price'] = df['Stock Price']/df['Strike Price']
df['Call Price'] = df['Call Price'] /df['Strike Price']
Data, libraries, activation functions¶
In [25]:
n = 300000
n_train = (int)(0.8 * n)
train = df[0:n_train]
X_train = train[['Stock Price', 'Maturity', 'Dividends', 'Volatility', 'Risk-free']].values
y_train = train['Call Price'].values
test = df[n_train+1:n]
X_test = test[['Stock Price', 'Maturity', 'Dividends', 'Volatility', 'Risk-free']].values
y_test = test['Call Price'].values
In [26]:
#Import libraries
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, LeakyReLU
from keras import backend
def custom_activation(x):
return backend.exp(x)
Set up, compile and fit the model¶
In [27]:
nodes = 120
model = Sequential()
model.add(Dense(nodes, input_dim=X_train.shape[1]))
#model.add("relu")
model.add(Dropout(0.25))
model.add(Dense(nodes, activation='elu'))
model.add(Dropout(0.25))
model.add(Dense(nodes, activation='relu'))
model.add(Dropout(0.25))
model.add(Dense(nodes, activation='elu'))
model.add(Dropout(0.25))
model.add(Dense(1))
model.add(Activation(custom_activation))
model.compile(loss='mse',optimizer='rmsprop')
model.fit(X_train, y_train, batch_size=64, epochs=10, validation_split=0.1, verbose=2)
Train on 216000 samples, validate on 24000 samples Epoch 1/10 - 8s - loss: 0.0057 - val_loss: 7.4883e-04 Epoch 2/10 - 7s - loss: 0.0015 - val_loss: 1.9140e-04 Epoch 3/10 - 7s - loss: 0.0011 - val_loss: 1.3774e-04 Epoch 4/10 - 7s - loss: 9.2811e-04 - val_loss: 1.8789e-04 Epoch 5/10 - 7s - loss: 8.1016e-04 - val_loss: 7.6661e-04 Epoch 6/10 - 7s - loss: 7.3763e-04 - val_loss: 4.5625e-04 Epoch 7/10 - 7s - loss: 6.8578e-04 - val_loss: 2.3756e-04 Epoch 8/10 - 6s - loss: 6.5888e-04 - val_loss: 3.1526e-04 Epoch 9/10 - 6s - loss: 6.3412e-04 - val_loss: 3.0274e-04 Epoch 10/10 - 6s - loss: 6.2144e-04 - val_loss: 1.6663e-04
Out[27]:
<keras.callbacks.History at 0x114aaba58>
Predict and check accuracy (in-sample)¶
In [36]:
y_train_hat = model.predict(X_train)
#reduce dim (240000,1) -> (240000,) to match y_train's dim
y_train_hat = squeeze(y_train_hat)
CheckAccuracy(y_train, y_train_hat)
Mean Squared Error: 0.00016682932578338937 Root Mean Squared Error: 0.012916242711539195 Mean Absolute Error: 0.010476568489765952 Mean Percent Error: 0.04828374053037054
Out[36]:
{'diff': array([0.01042038, 0.00506267, 0.01685324, ..., 0.01201171, 0.00689269,
0.01121564]),
'mse': 0.00016682932578338937,
'rmse': 0.012916242711539195,
'mae': 0.010476568489765952,
'mpe': 0.04828374053037054}
Predict and check accuracy (validation-sample)¶
In [37]:
y_test_hat = model.predict(X_test)
y_test_hat = squeeze(y_test_hat)
test_stats = CheckAccuracy(y_test, y_test_hat)
Mean Squared Error: 0.0001664824935001891 Root Mean Squared Error: 0.012902809519642964 Mean Absolute Error: 0.010449874111459336 Mean Percent Error: 0.04830276673827217
Random Forest of decision trees¶
A Random Forest uses several decision trees to make hypotheses about regions within subsamples of the data, then makes predictions based on the majority vote of these trees. This safeguards against overfitting/memorization of the training data.
Prepare Data¶
In [38]:
n = 300000
n_train = (int)(0.8 * n)
train = df[0:n_train]
X_train = train[['Stock Price', 'Maturity', 'Dividends', 'Volatility', 'Risk-free']].values
y_train = train['Call Price'].values
test = df[n_train+1:n]
X_test = test[['Stock Price', 'Maturity', 'Dividends', 'Volatility', 'Risk-free']].values
y_test = test['Call Price'].values
Fit Random Forest¶
In [40]:
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor()
forest = forest.fit(X_train, y_train)
y_test_hat = forest.predict(X_test)
In [41]:
stats = CheckAccuracy(y_test, y_test_hat)
Mean Squared Error: 5.1260407648828004e-05 Root Mean Squared Error: 0.007159637396462757 Mean Absolute Error: 0.005229974950943186 Mean Percent Error: 0.026802712584841782