%pylab inline
import pandas as pd
Populating the interactive namespace from numpy and matplotlib
Limited Dependent Variables¶
The dependent variable may be discrete, and could be binomial or multinomial. That is, the dependent variable is limited. In such cases, we need a different approach.
Discrete dependent variables are a special case of limited dependent variables. The Logit model we look at here is a discrete dependent variable model. Such models are also often called qualitative response (QR) models.
The Logistic Function¶
$$ y = \frac{1}{1+e^{-f(x_1,x_2,...,x_n)}} \in (0,1) $$
where
$$ f(x_1,x_2,...,x_n) = a_0 + a_1 x_1 + ... + a_n x_n \in (-\infty,+\infty) $$
#Sigmoid Function
def logit(fx):
return exp(fx)/(1+exp(fx))
fx = linspace(-4,4,100)
y = logit(fx)
plot(fx,y)
xlabel('f(x)')
ylabel('Logit value')
grid()
#Import the SBA Loans dataset
sba = pd.read_csv("data/SBA.csv")
print(sba.columns)
Index(['LoanID', 'GrossApproval', 'SBAGuaranteedApproval', 'subpgmdesc',
'ApprovalFiscalYear', 'InitialInterestRate', 'TermInMonths',
'ProjectState', 'BusinessType', 'LoanStatus', 'RevolverStatus',
'JobsSupported'],
dtype='object')
#Feature engineering
sba["GuaranteePct"] = sba.SBAGuaranteedApproval.astype("float")/sba.GrossApproval.astype("float")
X = sba[['ApprovalFiscalYear', 'InitialInterestRate', 'TermInMonths',
'RevolverStatus','JobsSupported','GuaranteePct']]
x1 = pd.get_dummies(sba.subpgmdesc)
#x1 = x1.drop(x1.columns[0],axis=1)
X = pd.concat([X,x1],axis=1)
x2 = pd.get_dummies(sba.BusinessType)
#x2 = x2.drop(x1.columns[0],axis=1)
X = pd.concat([X,x2],axis=1)
X.head()
| ApprovalFiscalYear | InitialInterestRate | TermInMonths | RevolverStatus | JobsSupported | GuaranteePct | 509 - DEALER FLOOR PLAN | Community Advantage Initiative | Community Express | Contract Guaranty | ... | Patriot Express | Revolving Line of Credit Exports - Sec. 7(a) (14) | Rural Lender Advantage | Seasonal Line of Credit | Small Asset Based | Small General Contractors - Sec. 7(a) (9) | Standard Asset Based | CORPORATION | INDIVIDUAL | PARTNERSHIP | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2006 | 11.25 | 84 | 1 | 4 | 0.50 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 2006 | 12.00 | 84 | 0 | 3 | 0.50 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 2 | 2006 | 12.00 | 84 | 0 | 4 | 0.50 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 2006 | 11.50 | 84 | 0 | 1 | 0.85 | 0 | 0 | 1 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 4 | 2006 | 11.50 | 84 | 0 | 1 | 0.85 | 0 | 0 | 1 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
5 rows × 26 columns
#Dependent categorical variable
y = pd.get_dummies(sba.LoanStatus)
y.head()
| CANCLD | CHGOFF | EXEMPT | PIF | |
|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 1 |
| 4 | 1 | 0 | 0 | 0 |
y.sum()
CANCLD 58970 CHGOFF 66649 EXEMPT 245083 PIF 156998 dtype: int64
idx1 = list(where(y.CHGOFF==1)[0])
idx2 = list(where(y.PIF==1)[0])
idx = append(idx1,idx2)
print(len(idx))
X = X.iloc[idx]
X["Intercept"] = 1.0
y = y.CHGOFF.iloc[idx]
223647
from sklearn.linear_model import LogisticRegression
from sklearn.cross_validation import train_test_split
from sklearn import metrics
from sklearn.cross_validation import cross_val_score
# instantiate a logistic regression model, and fit with X and y
model = LogisticRegression()
model = model.fit(X, y)
# check the accuracy on the training set
model.score(X, y)
/Users/srdas/anaconda3/lib/python3.6/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also note that the interface of the new CV iterators are different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)
0.8243750195620777
pd.DataFrame({'X':X.columns, 'Coeff':model.coef_[0]})
| X | Coeff | |
|---|---|---|
| 0 | ApprovalFiscalYear | -0.000533 |
| 1 | InitialInterestRate | 0.348134 |
| 2 | TermInMonths | -0.041177 |
| 3 | RevolverStatus | -0.345469 |
| 4 | JobsSupported | -0.000225 |
| 5 | GuaranteePct | 0.268519 |
| 6 | 509 - DEALER FLOOR PLAN | -0.004191 |
| 7 | Community Advantage Initiative | -0.000950 |
| 8 | Community Express | 0.467689 |
| 9 | Contract Guaranty | -0.022769 |
| 10 | EXPORT IMPORT HARMONIZATION | -0.002006 |
| 11 | FA$TRK (Small Loan Express) | -0.863875 |
| 12 | Guaranty | 0.609706 |
| 13 | Gulf Opportunity | -0.108411 |
| 14 | International Trade - Sec, 7(a) (16) | -0.000816 |
| 15 | Lender Advantage Initiative | -0.042409 |
| 16 | Patriot Express | 0.172032 |
| 17 | Revolving Line of Credit Exports - Sec. 7(a) (14) | -0.135843 |
| 18 | Rural Lender Advantage | -0.010936 |
| 19 | Seasonal Line of Credit | -0.003622 |
| 20 | Small Asset Based | -0.002782 |
| 21 | Small General Contractors - Sec. 7(a) (9) | -0.009936 |
| 22 | Standard Asset Based | -0.038550 |
| 23 | CORPORATION | 0.076209 |
| 24 | INDIVIDUAL | -0.034433 |
| 25 | PARTNERSHIP | -0.039321 |
| 26 | Intercept | 0.002332 |
Odds Ratio¶
What are odds ratios? An odds ratio (OR) is the ratio of probability of success to the probability of failure. If the probability of success is $p$, then
$$ OR = \frac{p}{1-p}; \quad \quad p = \frac{OR}{1+OR} $$
Odds Ratio Coefficients¶
In a linear regression, it is easy to see how the dependent variable changes when any right hand side variable changes. Not so with nonlinear models. A little bit of pencil pushing is required (add some calculus too).
The coefficient of an independent variable in a logit regression tell us by how much the log odds of the dependent variable change with a one unit change in the independent variable. If you want the odds ratio, then simply take the exponentiation of the log odds.
#Example
p = 0.3
OR = p/(1-p)
print('OR old =', OR)
beta = 2
OR_new = OR * exp(beta)
print('OR new =', OR_new)
p_new = OR_new/(1+OR_new)
print('p new =', p_new)
OR old = 0.4285714285714286 OR new = 3.1667383281131363 p new = 0.7600041276283266
# Evaluate the model by splitting into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
model2 = LogisticRegression()
model2.fit(X_train, y_train)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False)
# Predict class labels for the test set
predicted = model2.predict(X_test)
print(predicted)
[0 0 0 ... 1 1 1]
# Generate class probabilities
probs = model2.predict_proba(X_test)
print(probs)
[[0.93284152 0.06715848] [0.95486653 0.04513347] [0.83622947 0.16377053] ... [0.30179065 0.69820935] [0.43927039 0.56072961] [0.23599253 0.76400747]]
Metrics¶
Accuracy: the number of correctly predicted class values.
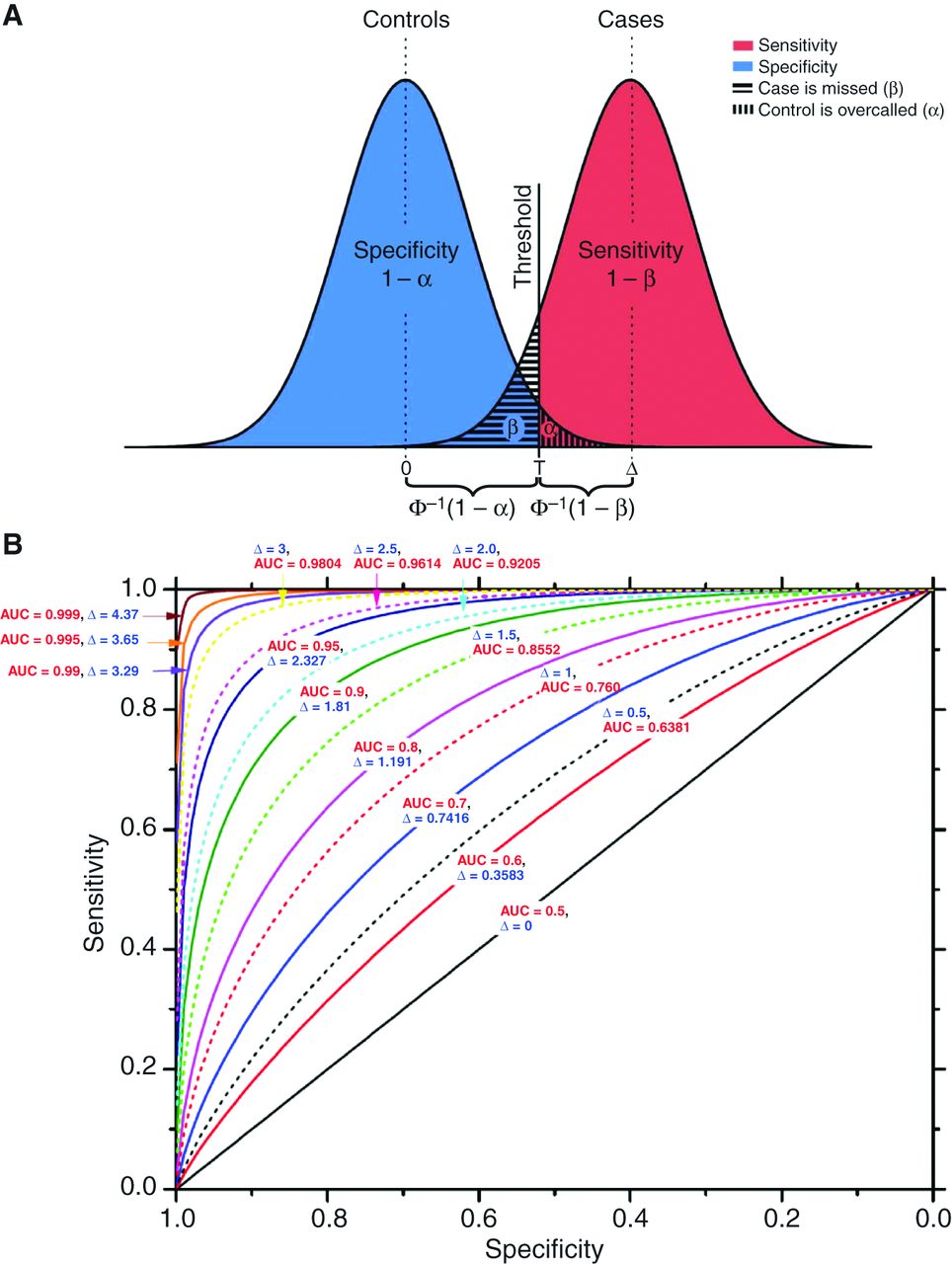
ROC and AUC: The Receiver-Operating Characteristic (ROC) curve is a plot of the True Positive Rate (TPR) against the False Positive Rate (FPR) for different levels of the cut-off posterior probability. This is an essential trade-off in all classification systems.
TPR = sensitivity or recall = TP/(TP+FN)
FPR = (1 − specificity) = FP/(FP+TN)
AUC of the ROC curve¶
# generate evaluation metrics
print(metrics.accuracy_score(y_test, predicted))
print(metrics.roc_auc_score(y_test, probs[:, 1]))
0.827066100305537 0.8600518349121413
More Metrics¶
Precision = $\frac{TP}{TP+FP}$
Recall = $\frac{TP}{TP+FN}$
F1 score = $\frac{2}{\frac{1}{Precision} + \frac{1}{Recall}}$
(F1 is the harmonic mean of precision and recall.)
print(metrics.confusion_matrix(y_test, predicted))
print(metrics.classification_report(y_test, predicted))
[[43753 3435]
[ 8168 11739]]
precision recall f1-score support
0 0.84 0.93 0.88 47188
1 0.77 0.59 0.67 19907
avg / total 0.82 0.83 0.82 67095
Using R¶
We can also use the R programming language as it if often better suited to econometrics.
We will use a basketball data set this time for a change of pace.
The rpy2 package allows us to call R from a Python notebook. https://rpy2.bitbucket.io/
#Load R interface
%load_ext rpy2.ipython
%%R
#Read in the data
ncaa = read.table("data/ncaa.txt",header=TRUE)
print(dim(ncaa))
head(ncaa)
[1] 64 14 No NAME GMS PTS REB AST TO A.T STL BLK PF FG FT X3P 1 1 NorthCarolina 6 84.2 41.5 17.8 12.8 1.39 6.7 3.8 16.7 0.514 0.664 0.417 2 2 Illinois 6 74.5 34.0 19.0 10.2 1.87 8.0 1.7 16.5 0.457 0.753 0.361 3 3 Louisville 5 77.4 35.4 13.6 11.0 1.24 5.4 4.2 16.6 0.479 0.702 0.376 4 4 MichiganState 5 80.8 37.8 13.0 12.6 1.03 8.4 2.4 19.8 0.445 0.783 0.329 5 5 Arizona 4 79.8 35.0 15.8 14.5 1.09 6.0 6.5 13.3 0.542 0.759 0.397 6 6 Kentucky 4 72.8 32.3 12.8 13.5 0.94 7.3 3.5 19.5 0.510 0.663 0.400
%%R
#Create the discrete dependent variable
y = c(rep(1,32),rep(0,32))
print(y)
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 [39] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
%%R
#FIT THE MODEL
x = as.matrix(ncaa[4:14])
h = glm(y~x, family=binomial(link="logit"))
names(h)
[1] "coefficients" "residuals" "fitted.values" [4] "effects" "R" "rank" [7] "qr" "family" "linear.predictors" [10] "deviance" "aic" "null.deviance" [13] "iter" "weights" "prior.weights" [16] "df.residual" "df.null" "y" [19] "converged" "boundary" "model" [22] "call" "formula" "terms" [25] "data" "offset" "control" [28] "method" "contrasts" "xlevels"
%%R
#RESULTS
summary(h)
Call:
glm(formula = y ~ x, family = binomial(link = "logit"))
Deviance Residuals:
Min 1Q Median 3Q Max
-1.80174 -0.40502 -0.00238 0.37584 2.31767
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -45.83315 14.97564 -3.061 0.00221 **
xPTS -0.06127 0.09549 -0.642 0.52108
xREB 0.49037 0.18089 2.711 0.00671 **
xAST 0.16422 0.26804 0.613 0.54010
xTO -0.38405 0.23434 -1.639 0.10124
xA.T 1.56351 3.17091 0.493 0.62196
xSTL 0.78360 0.32605 2.403 0.01625 *
xBLK 0.07867 0.23482 0.335 0.73761
xPF 0.02602 0.13644 0.191 0.84874
xFG 46.21374 17.33685 2.666 0.00768 **
xFT 10.72992 4.47729 2.397 0.01655 *
xX3P 5.41985 5.77966 0.938 0.34838
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 88.723 on 63 degrees of freedom
Residual deviance: 42.896 on 52 degrees of freedom
AIC: 66.896
Number of Fisher Scoring iterations: 6
Multinomial Logit¶
The probability of each class $(0,1,...,k)$ for $(k+1)$ classes is as follows:
$$ Pr[y=j] = \frac{e^{a_j^\top x}}{\sum_{i=1}^k e^{a_i^\top x}} $$
and
$$ Pr[y=0] = \frac{1}{\sum_{i=1}^k e^{a_i^\top x}} $$
Note that $\sum_{i=1}^k Pr[y=i] = 1$.
%%R
#CREATE 4 CLASSES THIS TIME
y = c(rep(3,16),rep(2,16),rep(1,16),rep(0,16))
print(y)
[1] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 [39] 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
%%R
#FIT THE MODEL
library(nnet)
res = multinom(y~x)
# weights: 52 (36 variable) initial value 88.722839 iter 10 value 71.549648 iter 20 value 61.992477 iter 30 value 51.299190 iter 40 value 45.868647 iter 50 value 44.083180 iter 60 value 43.077489 iter 70 value 42.899495 iter 80 value 42.810343 iter 90 value 42.801542 iter 100 value 42.784794 final value 42.784794 stopped after 100 iterations
%%R
#SHOW RESULTS
res
Call:
multinom(formula = y ~ x)
Coefficients:
(Intercept) xPTS xREB xAST xTO xA.T xSTL
1 33.74486 0.422694013 -0.4806896 -0.9195585 0.7372724 2.7309094 0.1447635
2 -36.50899 0.004284913 0.5255269 0.4297660 -0.5497475 -0.6485187 0.6165437
3 -37.22782 0.122753359 0.2754536 -0.3991256 -0.1922775 3.6335713 1.5423808
xBLK xPF xFG xFT xX3P
1 0.9647090 -0.70182622 -42.41196 -31.241416 4.455305
2 0.3488289 0.09580019 26.60137 1.879328 4.860927
3 0.3735845 -0.50986184 54.39210 -6.674520 9.199075
Residual Deviance: 85.56959
AIC: 157.5696
%%R
#SHOW FITTED PROBABILITIES
res$fitted.values
0 1 2 3 1 1.888050e-05 4.133988e-06 2.230529e-01 7.769241e-01 2 1.330803e-03 3.190942e-06 3.117341e-01 6.869319e-01 3 4.268885e-03 1.216086e-02 1.715465e-01 8.120238e-01 4 4.159952e-03 3.936794e-04 3.803861e-01 6.150603e-01 5 4.305721e-05 6.180023e-04 9.099103e-03 9.902398e-01 6 2.540295e-03 2.361934e-03 3.400121e-02 9.610966e-01 7 4.378465e-01 3.763472e-02 1.064833e-01 4.180354e-01 8 1.560960e-02 6.345346e-03 1.836137e-01 7.944314e-01 9 1.080259e-01 6.295627e-01 8.084915e-02 1.815622e-01 10 1.053989e-02 1.460114e-01 1.061839e-02 8.328303e-01 11 1.464710e-02 7.228643e-05 6.150862e-02 9.237720e-01 12 4.417163e-02 2.863110e-01 4.492631e-01 2.202543e-01 13 5.998852e-01 1.363305e-01 1.525843e-01 1.112001e-01 14 1.575963e-03 3.291118e-04 1.450963e-01 8.529986e-01 15 8.447668e-02 7.769070e-02 1.751230e-01 6.627097e-01 16 2.092274e-04 1.265544e-05 7.310815e-03 9.924673e-01 17 3.414007e-01 1.609382e-01 4.661578e-01 3.150324e-02 18 6.360953e-02 3.932566e-02 4.464439e-01 4.506209e-01 19 5.664264e-01 9.403579e-02 3.338793e-01 5.658492e-03 20 1.104658e-01 3.566126e-04 3.312751e-01 5.579025e-01 21 1.064146e-03 1.568687e-03 8.832741e-01 1.140931e-01 22 3.652745e-01 6.335649e-05 6.170933e-01 1.756882e-02 23 1.066821e-03 4.314891e-04 3.808451e-01 6.176566e-01 24 4.532601e-04 1.321951e-04 8.115169e-01 1.878977e-01 25 2.130672e-02 3.078825e-04 7.939373e-01 1.844481e-01 26 8.125162e-01 1.330343e-01 4.082831e-02 1.362120e-02 27 3.406127e-01 1.077831e-01 4.243325e-01 1.272717e-01 28 5.252339e-03 3.193172e-02 6.693308e-01 2.934852e-01 29 3.276303e-01 8.959376e-06 6.511549e-01 2.120583e-02 30 3.277192e-02 8.947956e-02 8.513615e-01 2.638705e-02 31 1.776614e-02 3.096287e-03 8.735734e-01 1.055642e-01 32 6.193828e-02 4.927497e-02 7.095201e-01 1.792667e-01 33 4.771668e-02 2.537225e-01 2.888593e-02 6.696748e-01 34 1.003055e-01 7.434172e-01 2.579348e-02 1.304838e-01 35 4.765748e-03 9.947628e-01 9.556859e-05 3.758403e-04 36 1.398686e-04 9.083478e-01 9.849835e-03 8.166247e-02 37 4.073354e-01 5.323330e-01 6.029327e-02 3.830930e-05 38 3.294020e-01 6.206803e-01 3.352896e-02 1.638879e-02 39 6.052431e-07 9.999427e-01 7.888562e-08 5.661504e-05 40 3.798824e-01 5.392550e-01 4.267431e-03 7.659525e-02 41 1.804106e-01 5.931465e-01 2.079838e-01 1.845914e-02 42 3.706691e-01 6.282619e-01 9.818912e-04 8.710775e-05 43 5.156512e-02 7.515302e-01 3.338974e-04 1.965708e-01 44 1.201667e-04 9.998380e-01 2.272071e-06 3.957491e-05 45 3.539251e-03 9.858485e-01 4.199784e-03 6.412445e-03 46 1.543950e-01 4.760056e-01 7.809938e-02 2.915000e-01 47 8.627304e-01 1.358509e-01 1.339768e-03 7.894795e-05 48 2.335101e-02 6.031354e-01 2.549603e-01 1.185533e-01 49 5.705300e-01 1.441831e-03 4.141977e-01 1.383048e-02 50 4.774755e-01 7.674058e-03 4.143597e-01 1.004908e-01 51 7.528071e-01 8.713894e-02 1.403245e-01 1.972942e-02 52 5.928981e-01 2.726977e-01 1.260571e-01 8.347137e-03 53 5.144014e-01 2.353508e-03 4.702759e-01 1.296916e-02 54 7.325728e-02 5.593682e-02 7.444625e-01 1.263434e-01 55 9.831852e-01 1.484960e-02 1.963491e-03 1.706239e-06 56 6.108326e-01 2.966325e-01 8.430316e-02 8.231720e-03 57 4.904276e-01 7.764094e-03 4.963668e-01 5.441490e-03 58 7.380363e-01 8.871521e-04 2.482101e-01 1.286648e-02 59 1.173954e-02 9.837496e-01 6.030581e-04 3.907765e-03 60 4.266638e-01 4.181472e-01 7.204418e-02 8.314481e-02 61 4.667043e-01 3.002245e-01 4.465928e-04 2.326247e-01 62 2.453611e-01 7.546104e-01 2.815524e-05 2.966871e-07 63 9.965619e-01 8.909688e-06 3.281234e-03 1.479751e-04 64 7.104700e-01 1.302820e-05 2.894608e-01 5.614299e-05