Machine Learning: A Quick Introduction

8. Machine Learning: A Quick Introduction#

A quick recap of machine learning before we get started with NLP.

8.1. Jupyter Extensions#

These allow using the notebooks in myriad ways, see: https://blog.jupyter.org/99-ways-to-extend-the-jupyter-ecosystem-11e5dab7c54

from google.colab import drive
drive.mount('/content/drive')  # Add My Drive/<>

import os
os.chdir('drive/My Drive')
os.chdir('Books_Writings/NLPBook/')

Mounted at /content/drive

%%capture
# %pylab inline
import pandas as pd
import os
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import Image

Image("NLP_images/ML_AI.png", width=700)

_images/b26d063c9ff8049f9ce4403698422cc01d3bd2fd4d81581f452640ea6e5f0b1c.png

https://medium.com/machine-learning-for-humans/why-machine-learning-matters-6164faf1df12

8.2. 5 Applications of ML in Finance#

https://www.verypossible.com/blog/5-applications-of-machine-learning-in-finance

https://towardsdatascience.com/machine-learning-in-finance-why-what-how-d524a2357b56

Image("NLP_images/ML_use_cases.jpg", width=600)

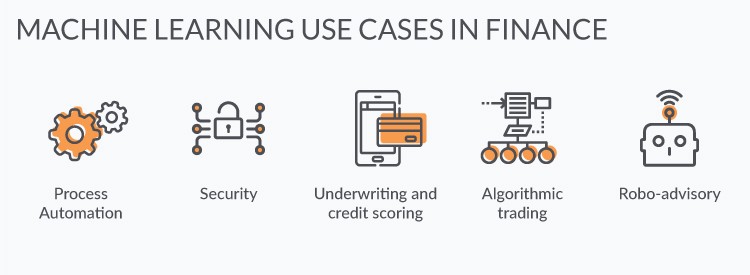
_images/708fccbed4ada02ff1b85dd580bad5adca509e16216a9d86fd5e85f0ace9cb90.jpg

Image("NLP_images/AI_solutions.jpg", width=600)

_images/c7388ddfe4085aa6ae505d6deaa2130c5de70a9c85d72cf56e93d18f96ca78e9.jpg

8.3. Many Applications of ML in Finance#

Fraud prevention
Risk management
Investment predictions
Customer service
Digital assistants
Marketing
Network security
Loan underwriting
Algorithmic trading
Process automation
Document interpretation
Content creation
Trade settlements
Money-laundering prevention
Custom machine learning solutions

https://igniteoutsourcing.com/fintech/machine-learning-in-finance/

For projects, start looking at Kaggle for finance datasets you may be able to use.

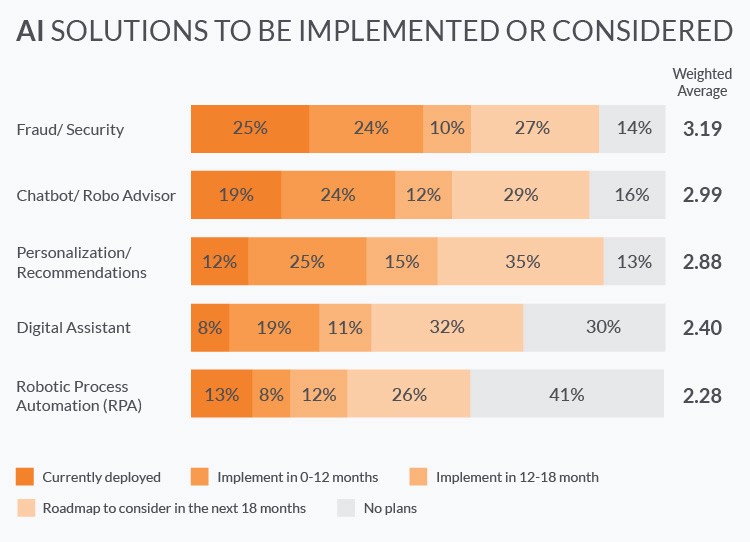
8.4. J.P. Morgan Guide to ML in Finance#

https://news.efinancialcareers.com/uk-en/285249/machine-learning-and-big-data-j-p-morgan

“You won’t need to be a machine learning expert, you will need to be an excellent quant and an excellent programmer

J.P. Morgan says the skillset for the role of data scientists is virtually the same as for any other quantitative researchers. Existing buy side and sell side quants with backgrounds in computer science, statistics, maths, financial engineering, econometrics and natural sciences should therefore be able to reinvent themselves. Expertise in quantitative trading strategies will be the crucial skill. “It is much easier for a quant researcher to change the format/size of a dataset, and employ better statistical and Machine Learning tools, than for an IT expert, silicon valley entrepreneur, or academic to learn how to design a viable trading strategy,” say Kolanovic and Krishnamacharc.”

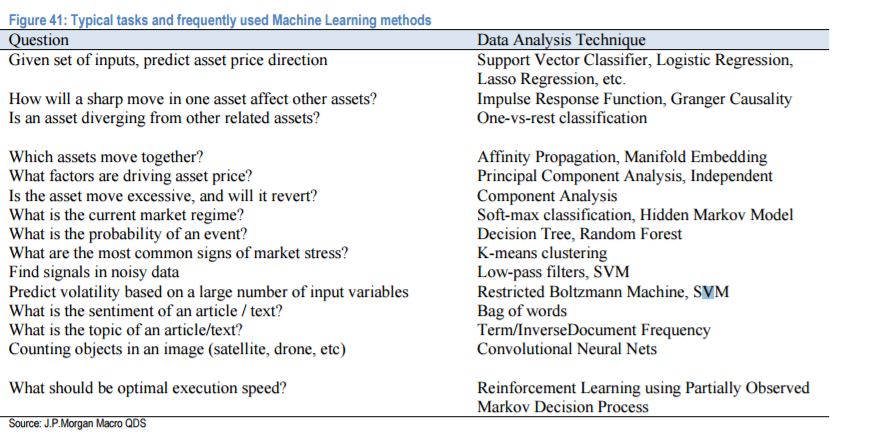
8.5. ML Tasks in Finance#

Image("NLP_images/JPMorgan-machine-learning-2.jpg", width=600)

_images/12a8834c4ef1b8f0226fc3203e8eba3b4ff32f8534617584521668c431aac7e4.jpg

8.6. ML with NLP#

Credit scoring, sentiment analysis, document search: https://emerj.com/ai-sector-overviews/natural-language-processing-applications-in-finance-3-current-applications/
Gather real-time intelligence on specific stocks; Provide key hire alerts; Monitor company sentiment; Anticipate client concerns; Upgrade quality of analyst reporting; Understand and respond to news events; Detect insider trading: https://www.ibm.com/blogs/watson/2016/06/natural-language-processing-transforming-financial-industry-2/
https://www.slideshare.net/QuantUniversity/nlp-in-finance
Ravenpack: https://www.ravenpack.com/; https://www.ravenpack.com/research/browse/

8.7. scikit-learn: Python’s one-stop shop for ML#

https://scikit-learn.org/stable/

8.8. Supervised Learning Models#

Linear Models
Logistic Regression
Discriminant Analysis
Bayes Classifier
Support Vector Machines
Nearest Neighbors (kNN)
Decision Trees
Neural Networks

8.9. Unsupervised Learning Models#

8.9.1. Clustering#

K-means
Hierarchical clustering

8.9.2. Dimension Reduction#

Principal Components Analysis
Factor Analysis
Autoencoders

8.10. Ensemble Methods#

Bagging
Stacking
Boosting

8.11. Small Business Association (SBA) Loans Dataset#

#Import the SBA Loans dataset
pd.set_option('display.max_columns', 500)
sba = pd.read_csv("NLP_data/SBA.csv")
print(sba.columns)
print(sba.shape)
sba.head()

Index(['LoanID', 'GrossApproval', 'SBAGuaranteedApproval', 'subpgmdesc',
       'ApprovalFiscalYear', 'InitialInterestRate', 'TermInMonths',
       'ProjectState', 'BusinessType', 'LoanStatus', 'RevolverStatus',
       'JobsSupported'],
      dtype='object')
(527700, 12)

	LoanID	GrossApproval	SBAGuaranteedApproval	subpgmdesc	ApprovalFiscalYear	InitialInterestRate	TermInMonths	ProjectState	BusinessType	LoanStatus	RevolverStatus	JobsSupported
0	733784	50000	25000	FA$TRK (Small Loan Express)	2006	11.25	84	IN	CORPORATION	CANCLD	1	4
1	733785	35000	17500	FA$TRK (Small Loan Express)	2006	12.00	84	IL	CORPORATION	CANCLD	0	3
2	733786	15000	7500	FA$TRK (Small Loan Express)	2006	12.00	84	WV	INDIVIDUAL	CANCLD	0	4
3	733787	16000	13600	Community Express	2006	11.50	84	MD	CORPORATION	PIF	0	1
4	733788	16000	13600	Community Express	2006	11.50	84	MD	CORPORATION	CANCLD	0	1

8.12. Feature Engineering#

#Feature engineering
sba["GuaranteePct"] = sba.SBAGuaranteedApproval.astype("float")/sba.GrossApproval.astype("float")
X = sba[['ApprovalFiscalYear', 'InitialInterestRate', 'TermInMonths',
        'RevolverStatus','JobsSupported','GuaranteePct']]

x1 = pd.get_dummies(sba.subpgmdesc, dtype=int)
X = pd.concat([X,x1],axis=1)

x2 = pd.get_dummies(sba.BusinessType, dtype=int)
X = pd.concat([X,x2],axis=1)

X.head()

	ApprovalFiscalYear	InitialInterestRate	TermInMonths	RevolverStatus	JobsSupported	GuaranteePct	Community Express	FA$TRK (Small Loan Express)	CORPORATION	INDIVIDUAL
0	2006	11.25	84	1	4	0.50	0	1	1	0
1	2006	12.00	84	0	3	0.50	0	1	1	0
2	2006	12.00	84	0	4	0.50	0	1	0	1
3	2006	11.50	84	0	1	0.85	1	0	1	0
4	2006	11.50	84	0	1	0.85	1	0	1	0

8.13. Logistic Regression (Logit)#

8.13.1. Limited Dependent Variables#

The dependent variable may be discrete, and could be binomial or multinomial. That is, the dependent variable is limited. In such cases, we need a different approach.
Discrete dependent variables are a special case of limited dependent variables. The Logit model we look at here is a discrete dependent variable model. Such models are also often called qualitative response (QR) models.

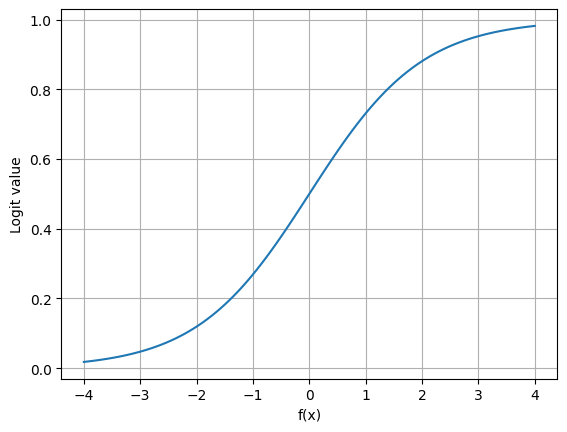
8.14. The Logistic Function#

\[ y = \frac{1}{1+e^{-f(x_1,x_2,...,x_n)}} \in (0,1) \]

where

\[ f(x_1,x_2,...,x_n) = a_0 + a_1 x_1 + ... + a_n x_n \in (-\infty,+\infty) \]

#Sigmoid Function
def logit(fx):
    return np.exp(fx)/(1+np.exp(fx))

fx = np.linspace(-4,4,100)
y = logit(fx)
plt.plot(fx,y)
plt.xlabel('f(x)')
plt.ylabel('Logit value')
plt.grid()

_images/508e06e09ff17183a9fdc927f7a56048a6cf01147bdb0d4301bc42cfcc8ed823.png

#Dependent categorical variable
y = pd.get_dummies(sba.LoanStatus, dtype=int)
y.head()

	CANCLD	PIF
0	1	0
1	1	0
2	1	0
3	0	1
4	1	0

#Prepare the X and y variables for chargeoffs vs paid in full
idx1 = list(np.where(y.CHGOFF==1)[0])
idx2 = list(np.where(y.PIF==1)[0])
idx = np.append(idx1,idx2)
print(len(idx))
X = X.iloc[idx]
# X["Intercept"] = 1.0

y = y.CHGOFF.iloc[idx]

#Save for later
y_SBA = y.copy()
X_SBA = X.copy()

y_SBA

	CHGOFF
5	1
8	1
9	1
11	1
14	1
...	...
508757	0
510524	0
510828	0
511814	0
514919	0

223647 rows × 1 columns

dtype: int64

X_SBA

	ApprovalFiscalYear	InitialInterestRate	TermInMonths	RevolverStatus	JobsSupported	GuaranteePct	509 - DEALER FLOOR PLAN	Community Advantage Initiative	Community Express	Contract Guaranty	EXPORT IMPORT HARMONIZATION	FA$TRK (Small Loan Express)	Guaranty	Gulf Opportunity	International Trade - Sec, 7(a) (16)	Lender Advantage Initiative	Patriot Express	Revolving Line of Credit Exports - Sec. 7(a) (14)	Rural Lender Advantage	Seasonal Line of Credit	Small Asset Based	Small General Contractors - Sec. 7(a) (9)	Standard Asset Based	CORPORATION	INDIVIDUAL	PARTNERSHIP
5	2006	11.50	28	0	2	0.85	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0
8	2006	11.25	46	1	6	0.50	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	1	0	0
9	2006	13.25	18	0	7	0.50	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	1	0	0
11	2006	12.25	32	0	2	0.50	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	1	0
14	2006	13.25	68	0	1	0.50	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	1	0	0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
508757	2015	5.00	12	1	5	0.50	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	1	0	0
510524	2015	5.50	6	0	0	0.50	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	1	0	0
510828	2015	6.00	60	0	12	0.85	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	1	0	0
511814	2015	5.21	84	0	4	0.50	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	1	0	0
514919	2015	8.75	84	1	0	0.50	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	1	0

223647 rows × 26 columns

%%time

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, roc_auc_score, confusion_matrix, classification_report
from sklearn.model_selection import cross_val_score

# instantiate a logistic regression model, and fit with X and y
model = LogisticRegression(penalty=None, max_iter=1000, tol=0.001) # higher number of iterations needed if the convergence rate is slow
model = model.fit(X, y)

# check the accuracy on the training set
model.score(X, y)

CPU times: user 35.4 s, sys: 360 ms, total: 35.7 s
Wall time: 21.6 s

0.8277464039311951

#Show the coefficients
pd.DataFrame({'X':X.columns, 'Coeff':model.coef_[0]})

	X	Coeff
0	ApprovalFiscalYear	-0.000784
1	InitialInterestRate	0.333744
2	TermInMonths	-0.042977
3	RevolverStatus	-0.340903
4	JobsSupported	-0.000136
5	GuaranteePct	-0.158797
6	509 - DEALER FLOOR PLAN	-0.054545
7	Community Advantage Initiative	-0.011115
8	Community Express	1.568193
9	Contract Guaranty	-0.306265
10	EXPORT IMPORT HARMONIZATION	-0.027013
11	FA$TRK (Small Loan Express)	-0.040360
12	Guaranty	1.654685
13	Gulf Opportunity	-1.292674
14	International Trade - Sec, 7(a) (16)	-0.009668
15	Lender Advantage Initiative	-0.496368
16	Patriot Express	1.574268
17	Revolving Line of Credit Exports - Sec. 7(a) (14)	-1.705447
18	Rural Lender Advantage	-0.096996
19	Seasonal Line of Credit	-0.048645
20	Small Asset Based	-0.037303
21	Small General Contractors - Sec. 7(a) (9)	-0.133505
22	Standard Asset Based	-0.508500
23	CORPORATION	0.180144
24	INDIVIDUAL	0.208657
25	PARTNERSHIP	-0.358629

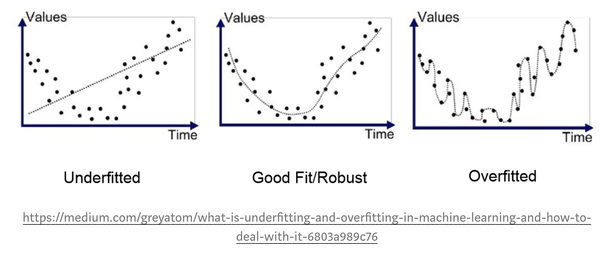
8.15. Training, validation, and testing data: Underfitting, Overfitting, Cross-Validation#

As we will see below, we split our data sample into training and testing subsets. Training data is used for machine learning a model and then the same model is applied to the test data (out-of-sample) to make sure the model performs well on data it has not already seen. The same model is also applied back to the same data on which it was trained. So, we get two accuracy scores, one on the training data set and another for the test data set. One hopes that a model performs as accurately on the test data as it does on the training data.

When accuracy is low on the training data, the model “underfits” the data. However, it may show a very high level of accuracy on the training data. This is a good thing, unless it achieves a very low accuracy level on the test data. In this case, we say that the model is “overfitted” to the data. The model is too specifically attuned to the training data so that it is useless for data outside the training data set. This occurs when the model has too many free parameters so it almost “memorizes” the training data set, which explains why it performs poorly on data it has not seen before. An analogy to this occurs when students memorize math homework problems without understanding the underlying concepts. When faced with a slightly different problem on the exam, they fail miserably.

We often break down a data sample into 3 types of data: training, validation, and testing data. Say we keep 20% of our data aside for testing. This is also known as “holdout” data. Of the remaining 80% data we may randomly sample 75% of it, and train the model so that it performs well on the remaining 25%. Then we randomly sample a different 75% and train to fit the remaining 25% starting from the current model or afresh. This is also called “rotation sampling”. If we repeat this $n$ times to get the best model, we are said to undertake “$n$-fold cross-validation”. The results are averaged to assess fit. Once a model has been trained through this cross-validated process, it is then taken to the test data to assess how well it performs and determination is made as to the extent of overfitting, if any.

The figure below provides a visual depiction of under- and over-fitting.

Image("NLP_images/overfitting.png", width=1000)

_images/7dde4f8c94d8029a1aa22d7ec0b3971fb9f4479f77b88178efcc8cfeb1d6129e.png

# Evaluate the model by splitting into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
model2 = LogisticRegression(penalty=None, max_iter=1000, tol=0.001)
model2.fit(X_train, y_train)

LogisticRegression(max_iter=1000, penalty=None, tol=0.001)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

# Predict class labels for the test set
predicted = model2.predict(X_test)
print(predicted)

[0 0 0 ... 1 1 1]

# Generate class probabilities
probs = model2.predict_proba(X_test)
print(probs)

[[0.93046744 0.06953256]
 [0.9527771  0.0472229 ]
 [0.83383113 0.16616887]
 ...
 [0.29892397 0.70107603]
 [0.41446059 0.58553941]
 [0.22209138 0.77790862]]

model2.score(X_test, y_test)

0.8288546091362993

8.16. Metrics#

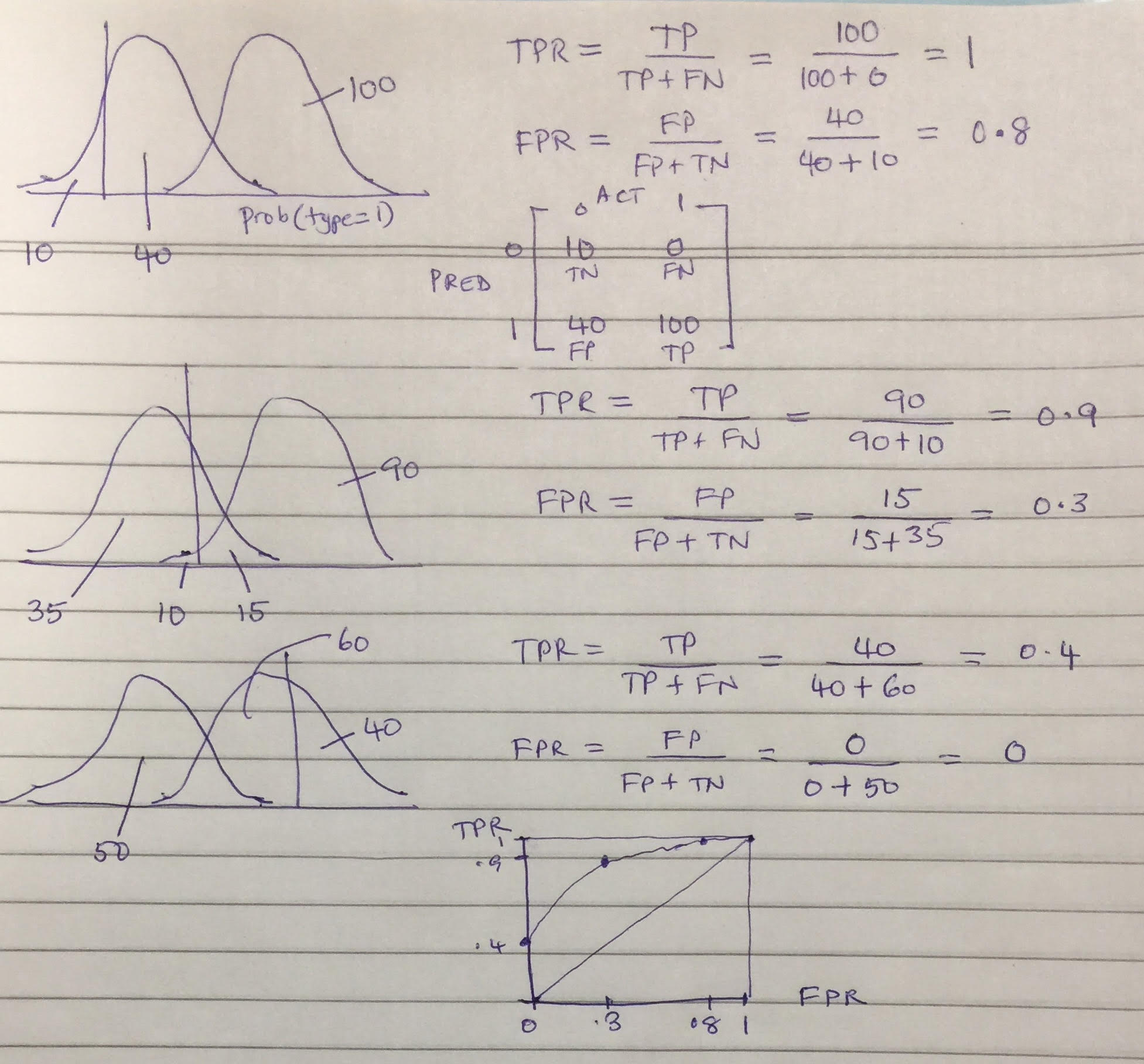
Accuracy: the number of correctly predicted class values.
TPR = sensitivity or recall = TP/(TP+FN)
FPR = (1 − specificity) = FP/(FP+TN)

# Confusion Matrix
CM = confusion_matrix(predicted, y_test) # predicted values on rows, true values on columns
CM

array([[43674,  7969],
       [ 3514, 11938]])

8.17. More Metrics#

Precision = $\frac{TP}{TP+FP}$
Recall = $\frac{TP}{TP+FN}$
F1 score = $\frac{2}{\frac{1}{Precision} + \frac{1}{Recall}}$

(F1 is the harmonic mean of precision and recall.)

print(classification_report(predicted, y_test))

              precision    recall  f1-score   support

           0       0.93      0.85      0.88     51643
           1       0.60      0.77      0.68     15452

    accuracy                           0.83     67095
   macro avg       0.76      0.81      0.78     67095
weighted avg       0.85      0.83      0.84     67095

8.18. The Matthews Correlation Coefficient#

https://en.wikipedia.org/wiki/Matthews_correlation_coefficient

This is a useful classification metric that is not widely used. See: https://towardsdatascience.com/the-best-classification-metric-youve-never-heard-of-the-matthews-correlation-coefficient-3bf50a2f3e9a

def MCC(tp,tn,fp,fn):
  return (tp*tn - fp*fn)/np.sqrt((tp+fp)*(tp+fn)*(tn+fp)*(tn+fn))

Let’s take the confusion matrix from above and apply the numbers therein to compute MCC.

print(CM)
mcc = MCC(CM[1,1], CM[0,0], CM[0,1], CM[1,0])
print("MCC =", mcc)

[[43674  7969]
 [ 3514 11938]]
MCC = 0.5698522319148718

8.19. ROC and AUC#

The Receiver-Operating Characteristic (ROC) curve is a plot of the True Positive Rate (TPR) against the False Positive Rate (FPR) for different levels of the cut-off posterior probability. This is an essential trade-off in all classification systems.

Image("NLP_images/roc_example.jpg", width=600)

_images/de2019e8f6378e4357a043f9ac3ff4d9956e569c5899d5580660c7f3e0b613c1.jpg

# generate evaluation metrics
print('Accuracy =', accuracy_score(y_test, predicted))
print('AUC =', roc_auc_score(y_test, probs[:, 1]))

Accuracy = 0.8288546091362993
AUC = 0.863604458068324

#ROC, AUC
from sklearn.metrics import roc_curve, auc
y_score = model.predict_proba(X_test)[:,1]
fpr, tpr, _ = roc_curve(y_test, y_score)

plt.title('ROC curve')
plt.xlabel('FPR (Precision)')
plt.ylabel('TPR (Recall)')

plt.plot(fpr,tpr)
plt.plot((0,1), ls='dashed',color='black')
plt.show()
print('Area under curve (AUC): ', auc(fpr,tpr))

_images/77452cfe269a9f6b89c3997dd6599c635d96bfb06a01ebe8c0a6b12c77f81cf8.png

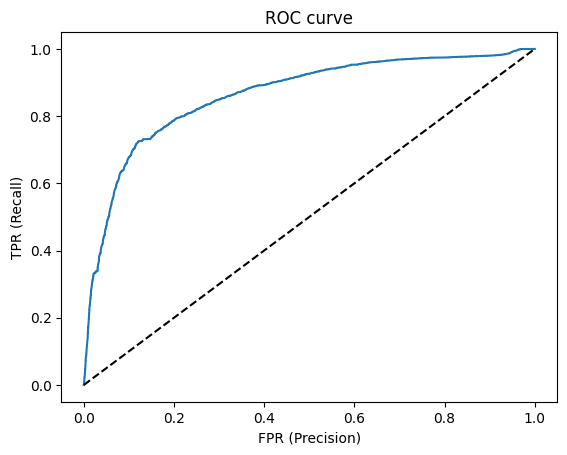
Area under curve (AUC):  0.8634953095597164

8.20. All In One#

A terrific article in Scientific American on ROC Curves by Swets, Dawes, Monahan (2000); pdf. And Dawes (1979) on the use of “Improper Linear Models”.

https://en.wikipedia.org/wiki/Receiver_operating_characteristic

Image("NLP_images/all_metrics.png", width=800)

_images/36b7913951c1d7e18af011be282b14866fed76f07751631ccd864edb7dff4b0f.png

8.21. ML Comic#

Google has put out an interesting comic book introduction to Machine Learning; pdf.
For a visual understanding of many ML concepts, Amazon has created https://www.amazon.science/latest-news/amazon-machine-learning-university-new-courses-mlu-explains